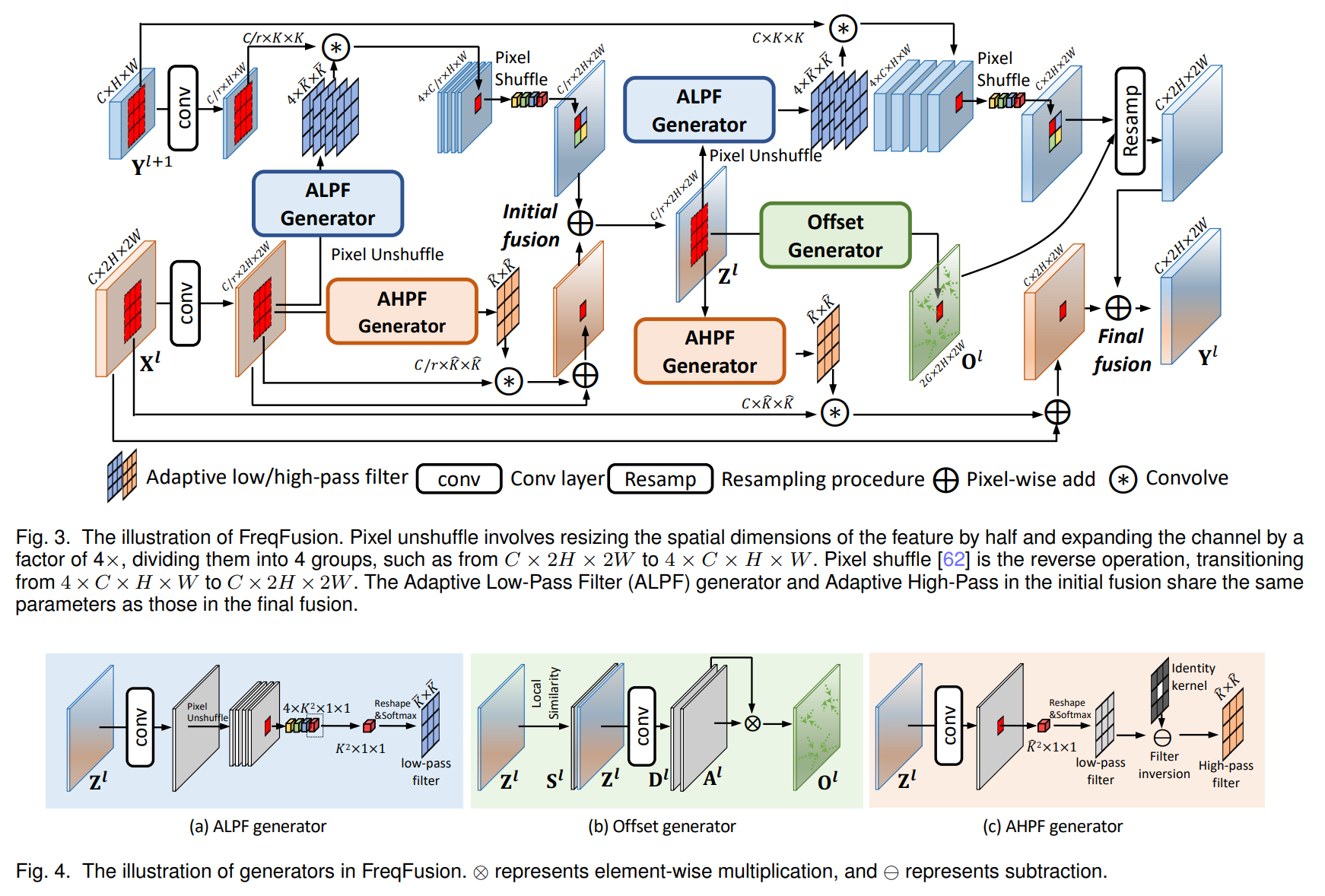
本文讨论了洛谷P3397题“地毯覆盖计数”的两种解法。作者最初用C语言暴力模拟遍历每个地毯覆盖的矩形区域,逐个累加计数,虽通过测试但效率较低。针对大规模数据(n、m≤1000),提出基于二维差分数组与前缀和的优化方案:通过标记地毯区域的四个顶点(左上角+1,右下角右侧和下侧各-1,并在右下角外补+1),将时间复杂度降为O(m+n²)。具体实现中,先对差分数组进行矩形范围标记,再通过两次前缀和计算(先逐行后逐列)得到最终覆盖次数。相比暴力法的O(mn²),差分法显著提升效率,适用于大范围网格问题,体现了二维差分处理区间叠加问题的核心思想。
![图片[1] - AI科研 编程 读书笔记 - 【算法】【Python】二维差分数组与其前缀和(洛谷P3397 地毯) - AI科研 编程 读书笔记 - 小竹の笔记本](https://img.smallbamboo.cn/i/2025/03/27/67e53c6d76f32.png)
这个题目我之前其实是做过的,当时使用的是C语言暴力模拟,居然没有TLE,代码如下:
#include <stdio.h>
int a[1000][1000]={0};
int main(){
int n,m;
int x1,x2,y1,y2;
scanf("%d %d",&n,&m);
while(m--){
scanf("%d %d %d %d",&x1,&y1,&x2,&y2);
x1--;x2--;y1--;y2--;
for (int i=x1;i<=x2;i++){
for (int j=y1;j<=y2;j++){
a[i][j]++;
}
}
}
for (int i=0;i<n;i++){
for (int j=0;j<n;j++){
printf("%d ",a[i][j]);
}
printf("\n");
}
}现在备赛蓝桥杯复习差分与前缀和时二次刷到了这个题目,看了当年用C写的代码根本没用到这个知识点,遍用Python又写了一遍:
n, m = map(int, input().strip().split())
data = [[0] * (n + 1) for _ in range(n + 1)]
for _ in range(m):
x1, y1, x2, y2 = map(int, input().strip().split())
data[x1-1][y1-1] += 1 # 左上角 +1
if x2 < n:
data[x2][y1-1] -= 1 # 下面一行 -1
if y2 < n:
data[x1-1][y2] -= 1 # 右侧一列 -1
if x2 < n and y2 < n:
data[x2][y2] += 1 # 右下角 +1
# 计算前缀和
for i in range(n):
for j in range(1, n):
data[i][j] += data[i][j-1]
for j in range(n):
for i in range(1, n):
data[i][j] += data[i-1][j]
for i in range(n):
print(" ".join(map(str, data[i][:n])))二维差分数组与其前缀和的关键(我自己认为的)是在使用二维差分数组时,矩形的右下角(x2, y2)需要进行特殊处理,以确保整个地毯的范围正确地更新。
对于矩形 (x1, y1, x2, y2):
- 左上角 (x1, y1) 加 1:表示这个矩形的开始。
- 右下角的右下 (x2+1, y2+1) 减 1:确保在这个点之后不受影响。
- 右侧 (x2+1, y1) 减 1:避免额外的列累加。
- 下侧 (x1, y2+1) 减 1:避免额外的行累加。
下面是一维查分与前缀和的模板:
2. 论文总结类文章中涉及的图表、数据等素材,版权归原出版商及论文作者所有,仅为学术交流目的引用;若相关权利人认为存在侵权,请联系本网站删除,联系方式:i@smallbamboo.cn。
3. 违反上述声明者,将依法追究其相关法律责任。























暂无评论内容