【人工智能】【Python】决策树实验

描述算法、数据集、及所设计的实验方案

这次实验是决策树算法，把决策树用到了分类与回归，并分析不同超参数及剪枝策略对模型性能的影响。分类任务选用经典的葡萄酒数据集，该数据集包含13个连续变量特征，涉及红酒的化学成分，对应三类不同品质的葡萄酒。回归任务则选用另一个加州房价数据集（California Housing），确保任务多样性与实验全面性。 在数据预处理中，针对缺失值，采用均值填充或删除策略；对类别变量，运用LabelEncoder或OneHotEncoder进行数值化编码。对于分类任务，进一步检验类别分布，若不均衡，则在训练集上施加SMOTE过采样，以避免模型过于偏离原始数据集。数据集划分为训练集与测试集，采用K折交叉验证增强模型泛化能力。（这里只在训练集上过采样是老师跟我说的，对我很有启发）

决策树模型构建方面，实验三个不同的决策树模型：

（1）预剪枝分类决策树，通过控制最大深度、最小样本分裂数等参数防止过拟合；

（2）后剪枝分类决策树，先训练完整树，再基于代价复杂度剪枝（CCP），优化泛化能力；

（3）预剪枝回归决策树，在回归任务中分析不同超参数的影响，并评估特征重要性。

网格搜索用于寻找最优分裂准则（信息增益、基尼系数等），并调优α参数以优化剪枝策略。最终，实验通过混淆矩阵、学习曲线、特征重要性分析等可视化手段，全面评估模型性能，使得实验能够把决策树分析透彻。

实验详细操作步骤或程序清单

# 导入必要的库
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns

# 设置 matplotlib 字体，防止中文乱码
plt.rcParams["font.sans-serif"] = ["Microsoft YaHei"]
plt.rcParams["figure.dpi"] = 120
plt.rcParams["font.size"] = 8

# 导入 scikit-learn 相关模块
from sklearn.datasets import load_wine, fetch_california_housing
from sklearn.model_selection import train_test_split, GridSearchCV, learning_curve, KFold
from sklearn.tree import DecisionTreeClassifier, DecisionTreeRegressor, plot_tree
from sklearn.metrics import (accuracy_score, precision_score, recall_score, f1_score,
                             confusion_matrix, mean_squared_error, r2_score,
                             classification_report)
# SMOTE 过采样
from imblearn.over_sampling import SMOTE

# ---------------------------
# 一、分类问题：使用葡萄酒数据集
# ---------------------------

# 加载葡萄酒数据集
wine = load_wine()
X_wine = pd.DataFrame(wine.data, columns=wine.feature_names)
y_wine = pd.Series(wine.target, name='target')

# 查看数据是否有缺失值
print("葡萄酒数据集缺失值统计：")
print(X_wine.isnull().sum())

# 检查类别分布（是否平衡）
print("\n类别分布：")
print(y_wine.value_counts())

# 划分训练集和测试集（测试集保持原始分布）
X_train, X_test, y_train, y_test = train_test_split(X_wine, y_wine, test_size=0.3,
                                                    random_state=42, stratify=y_wine)

# 若类别不平衡，可在训练集上使用 SMOTE 算法进行过采样
# 这里示例中葡萄酒数据集类别分布较均衡，但代码依然展示如何使用 SMOTE
smote = SMOTE(random_state=42)
X_train_smote, y_train_smote = smote.fit_resample(X_train, y_train)
print("\n使用 SMOTE 后，训练集类别分布：")
print(pd.Series(y_train_smote).value_counts())

# ---------------------------
# 二、预剪枝分类决策树（DecisionTreeClassifier）
# ---------------------------

# 定义预剪枝分类决策树的参数网格
param_grid_pre = {
    'max_depth': [3, 5, 7, 10, None],
    'min_samples_split': [2, 5, 10, 20],
    'min_samples_leaf': [1, 2, 5, 10],
    'criterion': ['gini', 'entropy']  # gini：基尼不纯度，entropy：信息增益
}

# 初始化 DecisionTreeClassifier
clf_pre = DecisionTreeClassifier(random_state=42)

# 使用 GridSearchCV 进行网格搜索（这里使用 5 折交叉验证）
grid_search_pre = GridSearchCV(clf_pre, param_grid_pre, cv=5, scoring='accuracy', n_jobs=-1)
grid_search_pre.fit(X_train_smote, y_train_smote)

# 输出最优参数及最佳得分
print("\n【预剪枝分类决策树】最优参数：", grid_search_pre.best_params_)
print("【预剪枝分类决策树】最佳交叉验证准确率：", grid_search_pre.best_score_)

# 用最优模型预测测试集
best_clf_pre = grid_search_pre.best_estimator_
y_pred_pre = best_clf_pre.predict(X_test)

# 计算评估指标
acc = accuracy_score(y_test, y_pred_pre)
precision = precision_score(y_test, y_pred_pre, average='macro')
recall = recall_score(y_test, y_pred_pre, average='macro')
f1 = f1_score(y_test, y_pred_pre, average='macro')
print("\n【预剪枝分类决策树】在测试集上的评估指标：")
print("准确率：", acc)
print("精确率（宏平均）：", precision)
print("召回率（宏平均）：", recall)
print("F1 分数（宏平均）：", f1)

# 绘制混淆矩阵
cm = confusion_matrix(y_test, y_pred_pre)
plt.figure(figsize=(5,4))
sns.heatmap(cm, annot=True, cmap="Blues", fmt='d')
plt.title("预剪枝分类决策树混淆矩阵")
plt.xlabel("预测标签")
plt.ylabel("真实标签")
plt.show()

# 绘制决策树结构（注意大树可能过于复杂）
plt.figure(figsize=(12,8))
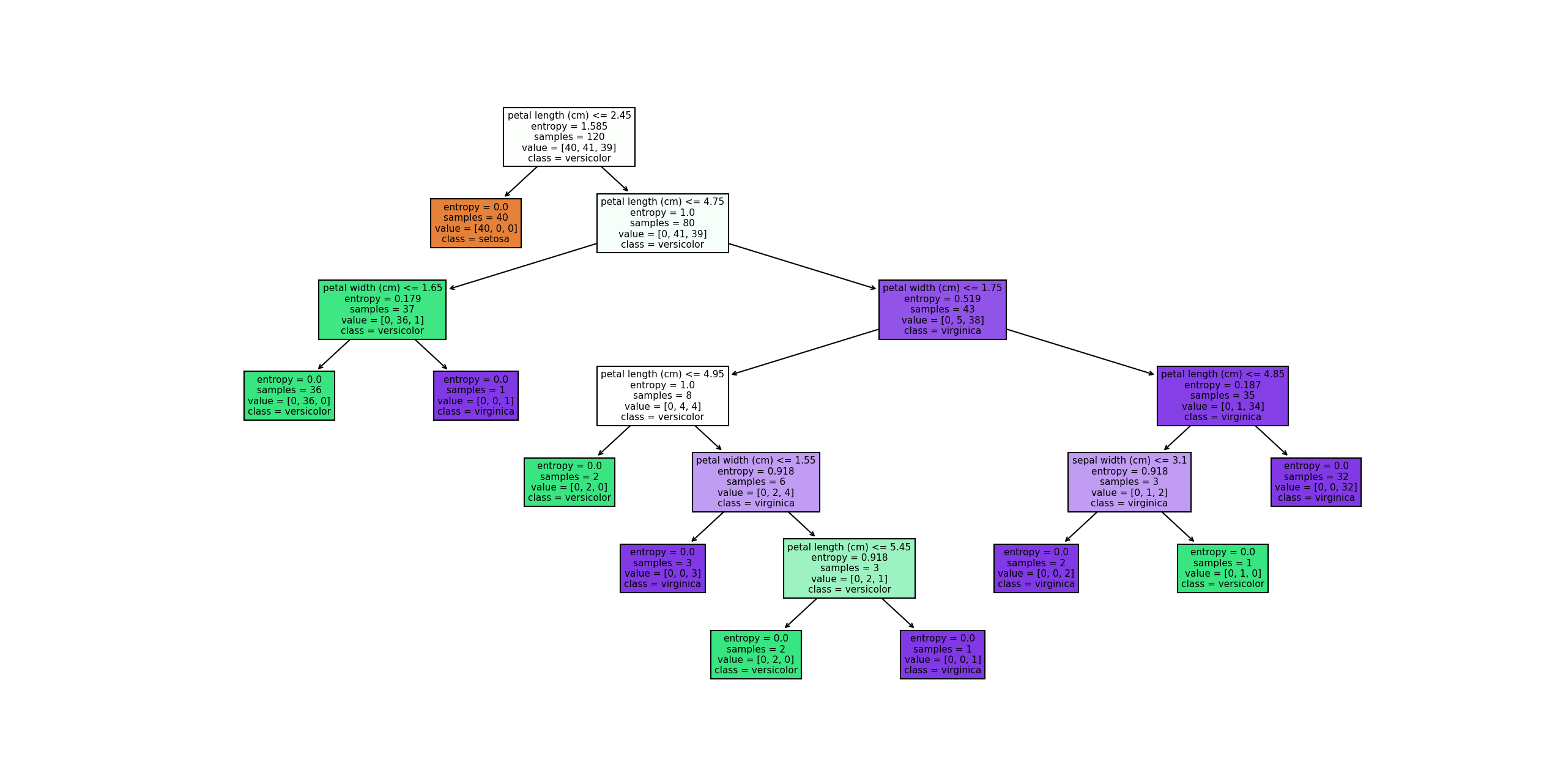
plot_tree(best_clf_pre, feature_names=wine.feature_names, class_names=wine.target_names, filled=True, fontsize=6)
plt.title("预剪枝分类决策树结构")
plt.show()

# 绘制学习曲线
train_sizes, train_scores, test_scores = learning_curve(best_clf_pre, X_train_smote, y_train_smote,
                                                        cv=5, scoring='accuracy', n_jobs=-1,
                                                        train_sizes=np.linspace(0.1, 1.0, 10))
plt.figure(figsize=(6,4))
plt.plot(train_sizes, np.mean(train_scores, axis=1), 'o-', color="r", label="训练集准确率")
plt.plot(train_sizes, np.mean(test_scores, axis=1), 'o-', color="g", label="交叉验证准确率")
plt.title("预剪枝分类决策树学习曲线")
plt.xlabel("训练样本数")
plt.ylabel("准确率")
plt.legend(loc="best")
plt.show()

# 分析特征重要性并绘制图形
importances = best_clf_pre.feature_importances_
indices = np.argsort(importances)[::-1]
plt.figure(figsize=(8,4))
plt.title("特征重要性")
plt.bar(range(X_wine.shape[1]), importances[indices], color="b", align="center")
plt.xticks(range(X_wine.shape[1]), np.array(wine.feature_names)[indices], rotation=45)
plt.tight_layout()
plt.show()

# ---------------------------
# 三、后剪枝分类决策树（DecisionTreeClassifier，增加 ccp_alpha 参数）
# ---------------------------

# 定义后剪枝的参数网格，增加剪枝复杂度参数 ccp_alpha
param_grid_post = {
    'criterion': ['gini', 'entropy'],
    'ccp_alpha': np.linspace(0.0001, 0.01, 10)  # 剪枝参数 α，值越大剪枝越严重
}

# 初始化后剪枝的分类决策树
clf_post = DecisionTreeClassifier(random_state=42)

# 使用 GridSearchCV 进行网格搜索
grid_search_post = GridSearchCV(clf_post, param_grid_post, cv=5, scoring='accuracy', n_jobs=-1)
grid_search_post.fit(X_train_smote, y_train_smote)

# 输出最优参数及最佳得分
print("\n【后剪枝分类决策树】最优参数：", grid_search_post.best_params_)
print("【后剪枝分类决策树】最佳交叉验证准确率：", grid_search_post.best_score_)

# 用最优模型预测测试集
best_clf_post = grid_search_post.best_estimator_
y_pred_post = best_clf_post.predict(X_test)

# 计算评估指标
acc_post = accuracy_score(y_test, y_pred_post)
precision_post = precision_score(y_test, y_pred_post, average='macro')
recall_post = recall_score(y_test, y_pred_post, average='macro')
f1_post = f1_score(y_test, y_pred_post, average='macro')
print("\n【后剪枝分类决策树】在测试集上的评估指标：")
print("准确率：", acc_post)
print("精确率（宏平均）：", precision_post)
print("召回率（宏平均）：", recall_post)
print("F1 分数（宏平均）：", f1_post)

# 绘制混淆矩阵
cm_post = confusion_matrix(y_test, y_pred_post)
plt.figure(figsize=(5,4))
sns.heatmap(cm_post, annot=True, cmap="Blues", fmt='d')
plt.title("后剪枝分类决策树混淆矩阵")
plt.xlabel("预测标签")
plt.ylabel("真实标签")
plt.show()

# 绘制决策树结构
plt.figure(figsize=(12,8))
plot_tree(best_clf_post, feature_names=wine.feature_names, class_names=wine.target_names, filled=True, fontsize=6)
plt.title("后剪枝分类决策树结构")
plt.show()

# ---------------------------
# 四、预剪枝回归决策树（DecisionTreeRegressor）
# ---------------------------

# 加载回归数据集：使用 California Housing 数据集
housing = fetch_california_housing(as_frame=True)
X_housing = housing.data
y_housing = housing.target

# 检查缺失值
print("\nCalifornia Housing 数据集缺失值统计：")
print(X_housing.isnull().sum())

# 划分训练集和测试集（不需要进行 SMOTE 过采样，回归问题不涉及类别不平衡）
X_train_reg, X_test_reg, y_train_reg, y_test_reg = train_test_split(X_housing, y_housing,
                                                                    test_size=0.3,
                                                                    random_state=42)

# 定义预剪枝回归决策树的参数网格
param_grid_reg = {
    'max_depth': [3, 5, 7, 10, None],
    'min_samples_split': [2, 5, 10, 20],
    'min_samples_leaf': [1, 2, 5, 10],
    'criterion': ['squared_error', 'friedman_mse']  # 两种误差衡量方法
}

# 初始化回归决策树
reg = DecisionTreeRegressor(random_state=42)

# 使用 GridSearchCV 进行网格搜索（这里使用 5 折交叉验证，评价指标为负均方误差）
grid_search_reg = GridSearchCV(reg, param_grid_reg, cv=5, scoring='neg_mean_squared_error', n_jobs=-1)
grid_search_reg.fit(X_train_reg, y_train_reg)

# 输出最优参数及最佳得分（注意均方误差取负值）
print("\n【预剪枝回归决策树】最优参数：", grid_search_reg.best_params_)
print("【预剪枝回归决策树】最佳交叉验证均方误差（负值）：", grid_search_reg.best_score_)

# 用最优模型预测测试集
best_reg = grid_search_reg.best_estimator_
y_pred_reg = best_reg.predict(X_test_reg)

# 计算评估指标：均方误差和 R2 分数
mse_reg = mean_squared_error(y_test_reg, y_pred_reg)
r2_reg = r2_score(y_test_reg, y_pred_reg)
print("\n【预剪枝回归决策树】在测试集上的评估指标：")
print("均方误差：", mse_reg)
print("R2 得分：", r2_reg)

# 绘制回归决策树的结构
plt.figure(figsize=(12,8))
plot_tree(best_reg, feature_names=housing.feature_names, filled=True, fontsize=6)
plt.title("预剪枝回归决策树结构")
plt.show()

# 绘制回归决策树的学习曲线
train_sizes_reg, train_scores_reg, test_scores_reg = learning_curve(best_reg, X_train_reg, y_train_reg,
                                                                    cv=5, scoring='neg_mean_squared_error', n_jobs=-1,
                                                                    train_sizes=np.linspace(0.1, 1.0, 10))
plt.figure(figsize=(6,4))
plt.plot(train_sizes_reg, -np.mean(train_scores_reg, axis=1), 'o-', color="r", label="训练集均方误差")
plt.plot(train_sizes_reg, -np.mean(test_scores_reg, axis=1), 'o-', color="g", label="交叉验证均方误差")
plt.title("预剪枝回归决策树学习曲线")
plt.xlabel("训练样本数")
plt.ylabel("均方误差")
plt.legend(loc="best")
plt.show()

实验结果(上传实验结果截图或者简单文字描述)

注意：加州房价数据集比较大，生成的决策树较为复杂：

以下是整体的程序文本输出：

D:\AnacondaEnvs\PyTorch\python.exe D:\桌面\编程相关\04_IDE练习项目\sklearn\scikit-learn\Lab\lab020.py
葡萄酒数据集缺失值统计：
alcohol 0
malic_acid 0
ash 0
alcalinity_of_ash 0
magnesium 0
total_phenols 0
flavanoids 0
nonflavanoid_phenols 0
proanthocyanins 0
color_intensity 0
hue 0
od280/od315_of_diluted_wines 0
proline 0
dtype: int64

类别分布：
target
1 71
0 59
2 48
Name: count, dtype: int64

使用 SMOTE 后，训练集类别分布：
target
0 50
1 50
2 50
Name: count, dtype: int64

【预剪枝分类决策树】最优参数： {'criterion': 'entropy', 'max_depth': 3, 'min_samples_leaf': 1, 'min_samples_split': 2}
【预剪枝分类决策树】最佳交叉验证准确率： 0.9533333333333334

【预剪枝分类决策树】在测试集上的评估指标：
准确率： 0.9074074074074074
精确率（宏平均）： 0.907843137254902
召回率（宏平均）： 0.9153439153439153
F1 分数（宏平均）： 0.909944831591173

【后剪枝分类决策树】最优参数： {'ccp_alpha': 0.0001, 'criterion': 'entropy'}
【后剪枝分类决策树】最佳交叉验证准确率： 0.9533333333333334

【后剪枝分类决策树】在测试集上的评估指标：
准确率： 0.9074074074074074
精确率（宏平均）： 0.907843137254902
召回率（宏平均）： 0.9153439153439153
F1 分数（宏平均）： 0.909944831591173

California Housing 数据集缺失值统计：
MedInc 0
HouseAge 0
AveRooms 0
AveBedrms 0
Population 0
AveOccup 0
Latitude 0
Longitude 0
dtype: int64

【预剪枝回归决策树】最优参数： {'criterion': 'friedman_mse', 'max_depth': None, 'min_samples_leaf': 10, 'min_samples_split': 2}
【预剪枝回归决策树】最佳交叉验证均方误差（负值）： -0.3960175472025311

【预剪枝回归决策树】在测试集上的评估指标：
均方误差： 0.3813276807925977
R2 得分： 0.7094735021638856

进程已结束，退出代码为 0

疑难小结(总结个人在实验中遇到的问题或者心得体会)

这次实验挺有意思的，让我对决策树的构建、优化，以及剪枝策略的实际影响有了更直观的理解。刚开始，我还以为调整 max_depth、min_samples_split 这些参数就能把决策树调到最优，但实验过程中，我发现光靠这些预剪枝手段，虽然能有效防止树过深导致的过拟合，却可能错失关键信息，影响模型的学习能力。于是，我又去请教了老师，问能不能把 max_depth 这些参数和 α（后剪枝的一个参数）放在一起调优。老师听完笑了笑，说：“这些是两个不同的剪枝方式，max_depth 这些是预剪枝，而 α 属于后剪枝，思路完全不一样。”这句话瞬间点醒了我，剪枝不只是简单的“修剪”，更像是两种不同的建模思维：要么提前限制树的生长，要么先让它自由生长，再回头修剪。 

实验过程中，不同的分裂准则（信息增益、基尼系数等）在数据分布不均衡的情况下差异很明显。SMOTE 过采样在平衡类别上起到了作用，但偶尔会引入噪声，导致某些分类边界变得模糊。后剪枝虽然能有效减少噪声的干扰，但 α 的取值需要特别谨慎，调大了会过度修剪，模型变得太简单，调小了又没什么作用。 最后，混淆矩阵让我清楚地看到模型在哪些类别上容易出错，而学习曲线则展示了模型的拟合情况。

但真正让我头疼的是，如何在模型复杂度和泛化能力之间找到最佳平衡：这个问题没有标准答案，每个数据集的情况都不同。也许结合特征选择、甚至用集成学习的方法，会是进一步优化的方向。

总之，这次实验让我对决策树的剪枝的方法有了更深的体会，模型调优不只是参数堆砌，而是对数据特征、模型结构、泛化能力的全面权衡。