【人工智能】重磅！近期人工智能原理学习总结 - AI科研编程读书笔记

很久之前就认识了Ele实验室这个UP主，也推荐大家去学习，他的视频大多为计算机软硬件科普，技术力和视频质量可谓十分强悍。

看到他有一个叫“小白也能听懂的人工智能原理”的课程，于是我就在网上找到了盗版学习（正版舍不得买，现在来总结学习成果。

初识神经网络

McCulloch-Pitts神经元模型 && Rosenblatt感知器。

McCulloch-Pitts神经元模型是神经科学领域里的经典模型，被视为人工神经网络的基础之一。它最初由Warren McCulloch和Walter Pitts在1943年提出，被用来描述生物神经元的基本工作原理。

Rosenblatt感知器是基于McCulloch-Pitts神经元模型的一个扩展，由Frank Rosenblatt在1957年提出。它引入了一些新的概念，例如权重的自动更新和阈值的调整，使得它更适合于机器学习任务。

一元一次函数感知器

如何描述一个直觉？可以使用函数来描述认知。把智能体对世界认知的过程看作在脑中不断形成各种函数。视频中的案例：豆豆的毒性与其大小有关，这里的直觉自然是一元一次函数。y=wx，x是大小，y是毒性，而w是确定的参数（斜率，权重）。这就是McCulloch-Pitts神经元模型，这个模型是对生物神经元相当简单的模仿。树突输入x，被权值参数w扩大或缩小，然后输出。完整的McCulloch-Pitts模型还有一个偏置项b，在一次函数后还会加一个激活函数，用来激活神经元的输出。

随着w取不同值，函数会出很多错误，问题是w设置为多少才能够很好的预测呢？作为有智能的人类，我们知道需要调节w，机器可不会知道。于是，Rosenblatt感知器出现了，可以让神经元自己调整参数。输入通过McCulloch-Pitts神经元模型后输出一个结果，用标准答案减去这个结果得到误差，然后用误差累加到w，若预测过大误差为负数，w变小。这就是通过误差修正参数w。

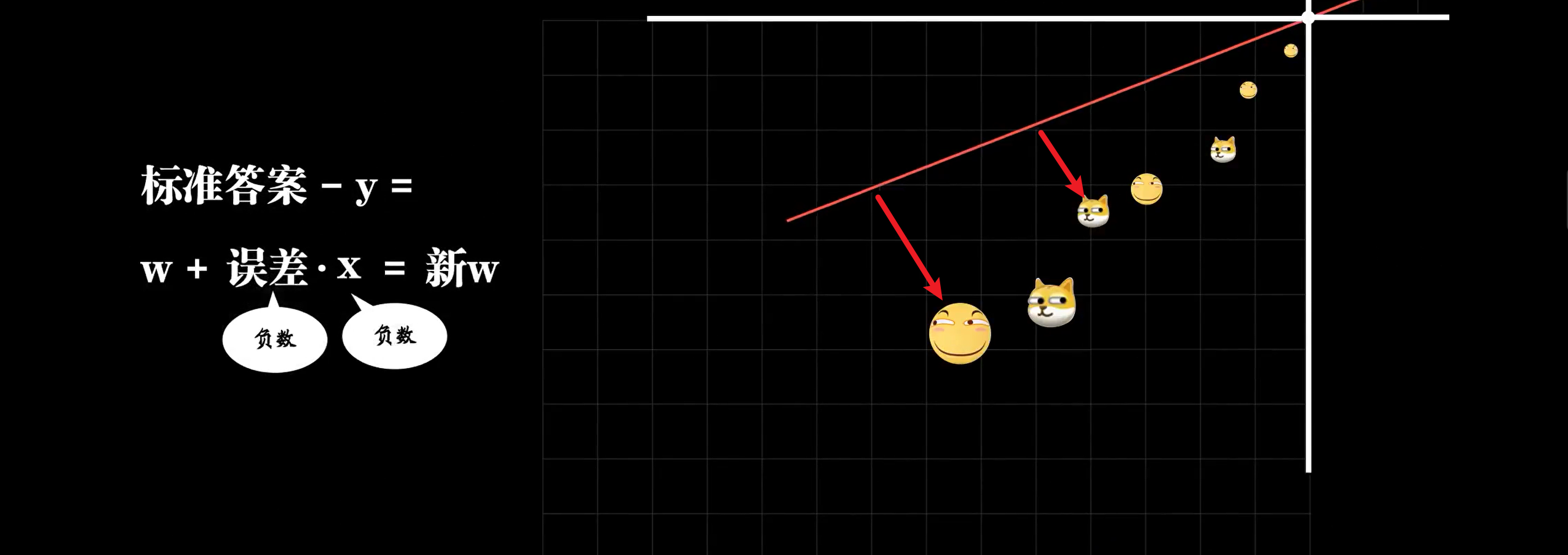
但在Rosenblatt感知器模型中误差还要乘以输入x，豆豆的大小只能是正值，但是若输入数据为负数，恰恰相反，所以让x乘以误差，若x为负数时，预测过大时，误差为负数，乘以x为正值，w增大。

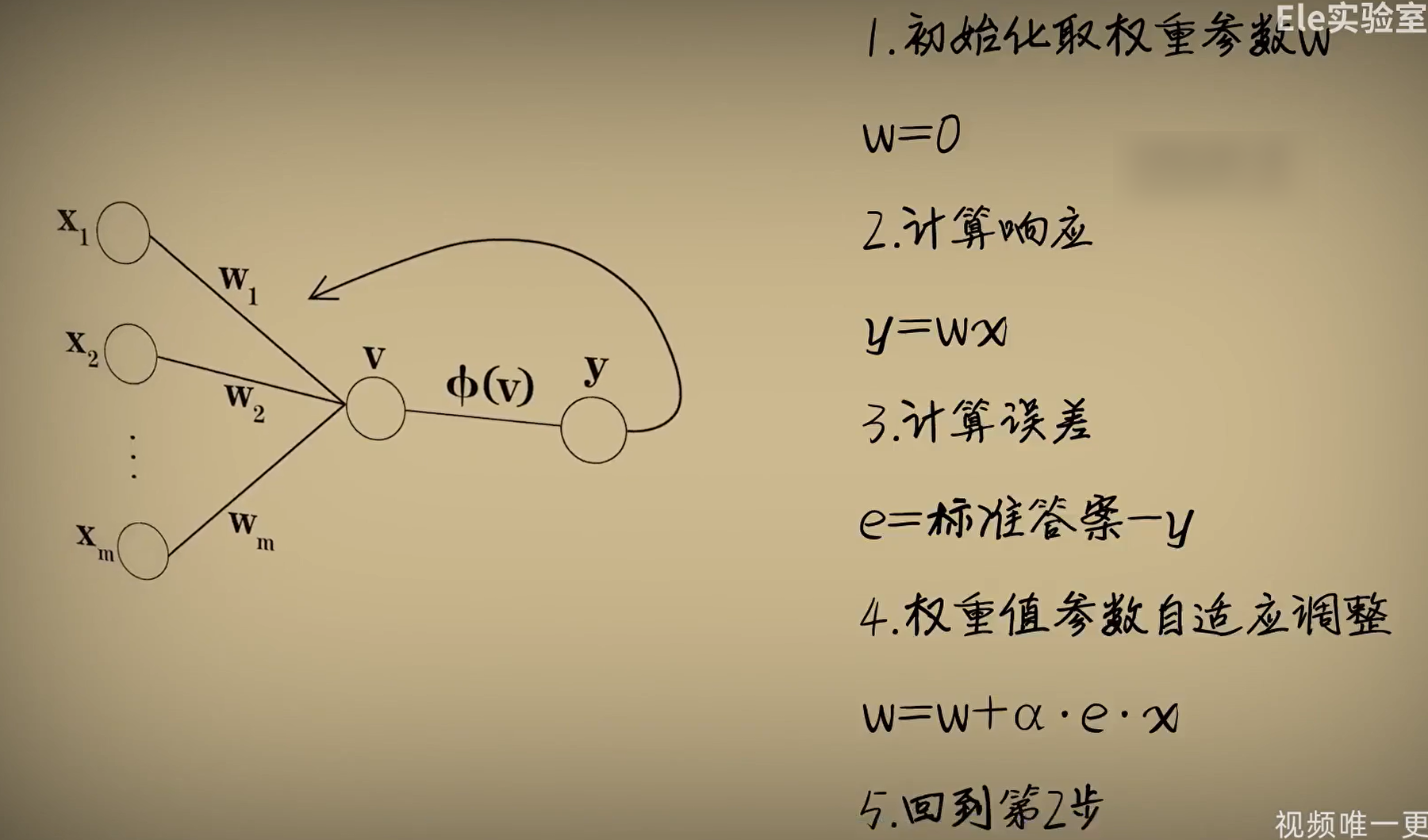
当然除了要乘以x外，Rosenblatt感知器模型还让误差乘以一个系数alpha（学习率）。让误差乘以学习率是为了防止调整幅度过大，错过最佳点。而太小的学习率会让学习过程太慢。

方差代价函数

如何评估差值？使用差值吗？这样并不好，若两个数据正好关于预测曲线对称，那么他们的差值互为相反数，这样加起来误差为0？当然不是完美预测了。差值有正负会有抵消的问题。

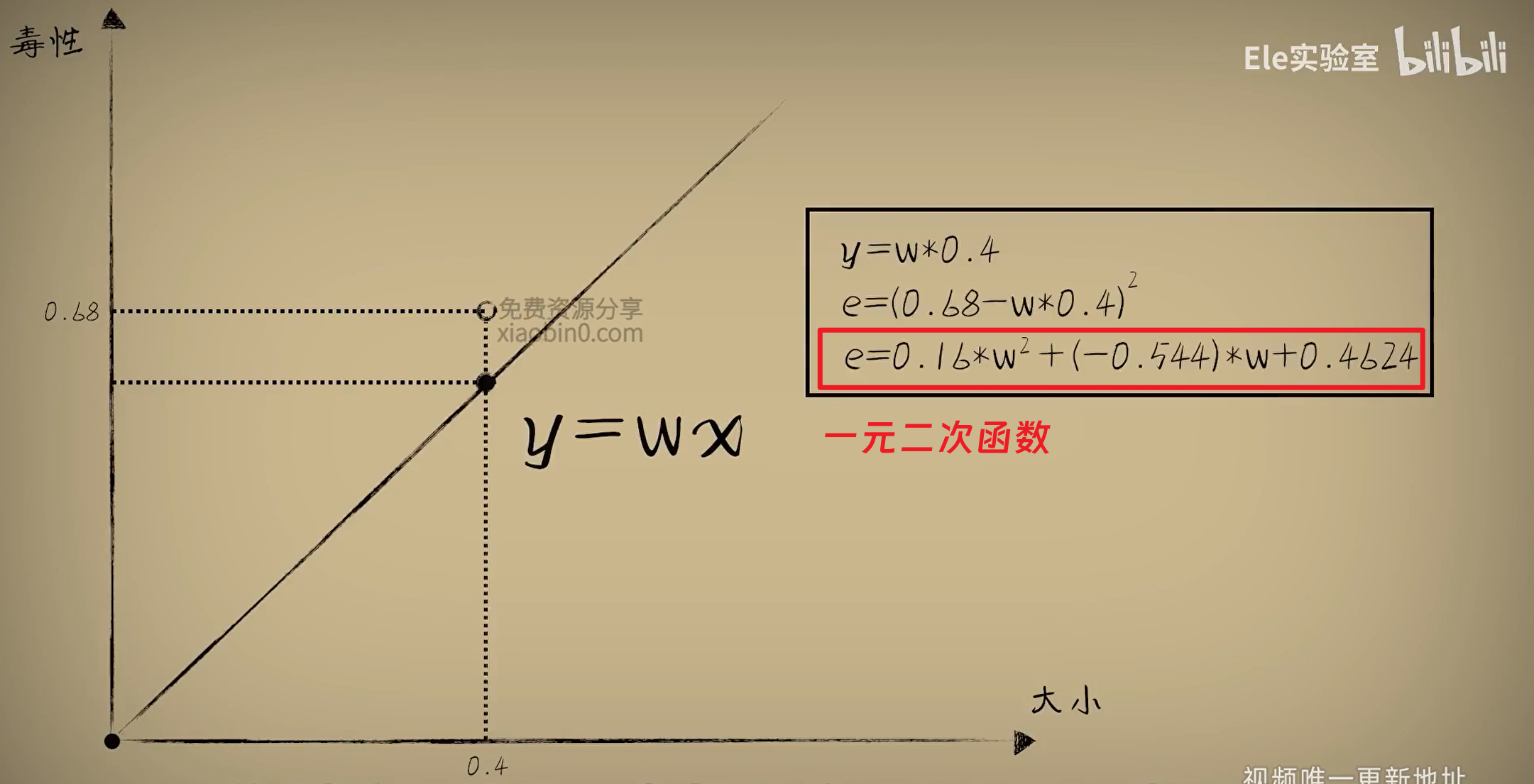
更好的误差评估方式：平方误差（差值取平方）。平方误差-w图像是一个开口向上的一元二次函数。在整体上来，我们需要取各个平方误差的平均值，所以e也叫做均方误差，这个e-w图像也就叫做方差代价函数（用于分析并改进预测函数的辅助函数）。由于事物出现的频率收敛于它的概率，我们现在需要研究的就是先预设一个w，然后统计大量数据去评估w是否合适，这就是回归分析，评估的标准就是“均方误差”，并试图让它最小，也就是回归分析中的“最小二乘法”。

把代价函数中最低点的w值放回预测函数中，这时预测函数就很好的完成了对数据的拟合。

如何让机器自己去找到e的最低点x呢？可以使用二次函数的对称轴w=-b/2a。一次性求解出让误差最小的w取值的方法叫做正规方程。但是如果有海量数据时，非常消耗计算资源，使用正规方程显然就不合适了，更常用的方法是梯度下降。

梯度下降和反向传播

梯度下降

使用一点点挪动的方式找到最低点。在最低点的左边需要把w调大，右边需要把w调小。左边的斜率是负数，右边的斜率是正数，这样就可以判断当前在左边还是右边。一元二次函数的斜率是怎么求的？导数（极限/微分）啊！

每次调整多少合适呢？先试试每次调整0.01吧！我们可以发现一开始下降的过程很慢，最后的点在最低处不断震荡。这是因为每次调整的都是呆板的0.01，当w距离最低点远的时候让它调整的快一些，在距离最低点近的时候让它慢下来。我们发现：越远的地方斜率的绝对值越大，越近的地方斜率的绝对值越小。新w=w-斜率，这时候你会发现w反复横跳，此时此刻恰如彼时彼刻。在Rosenblatt感知器做参数调整时，调整过程太震荡了。相似的，给斜率乘上一个小的学习率alpha，这样就可以实现我们的想法了。这种根据曲线不同处“斜率”去调整w的方式叫做“梯度下降”，梯度比斜率更广泛，之后会有三维空间中的梯度下降。梯度下降算法能在不断训练中让误差代价逐渐向最低点移动。

每次取一个样本的梯度下降，收敛的过程是随机震荡的轨迹，所以也叫做“随机梯度下降”。

（mini batch）迷你批量梯度下降：每次选样本中的一小批进行梯度下降。

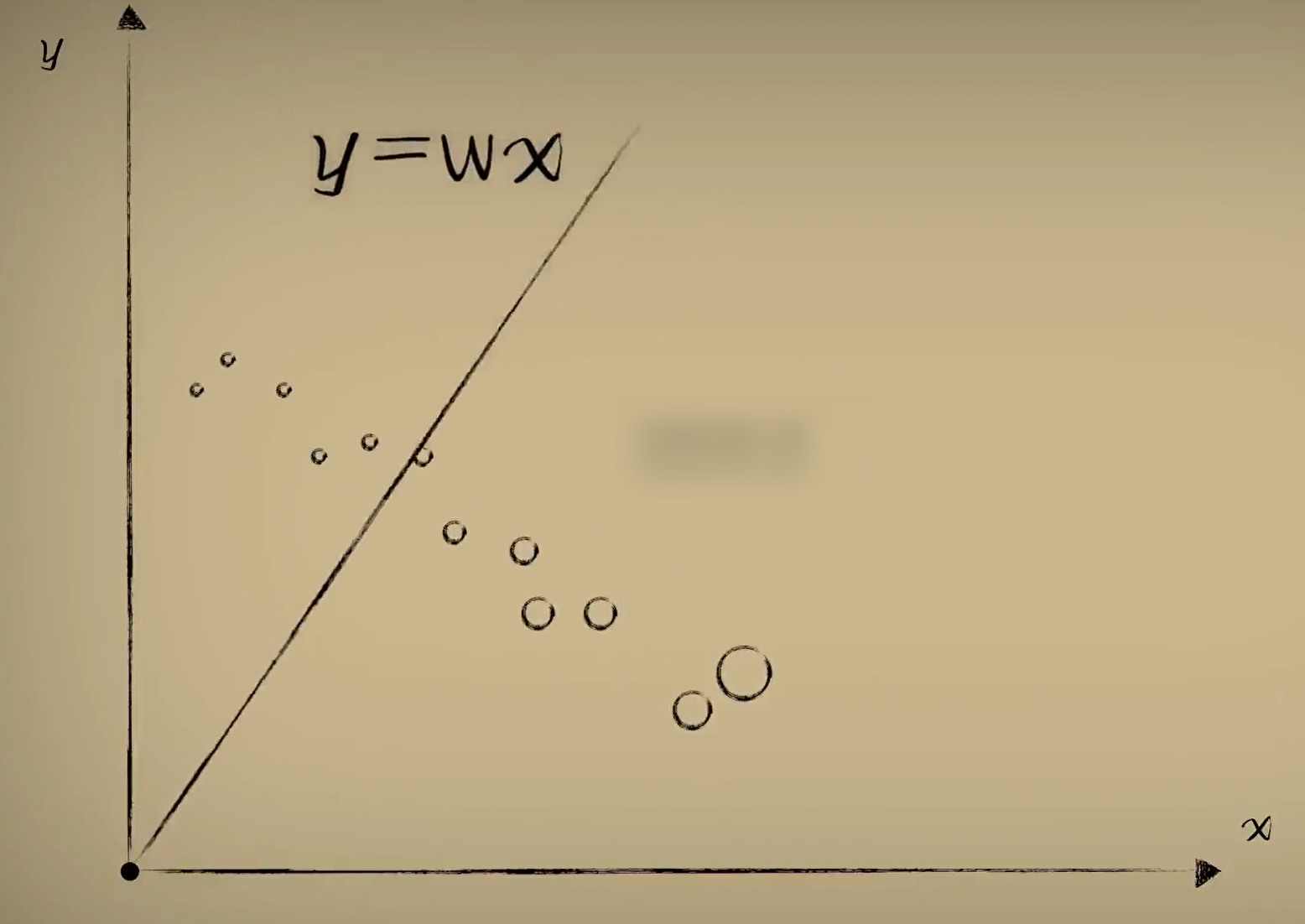
现在有一个问题，y=wx这样的预测函数灵活性很低，因为它必须要过原点，完整的函数是y=wx+b。现在的预测函数有了新的一项b，这样就会导致方差代价函数多了一个元，这样方差代价函数就变成了三维的。

这个碗装曲面的最低点意味着w和b在预测函数中最合适的值，也就是此刻的w和b会让e最小。如何找到这个碗装曲面的最低点呢？梯度下降！现在需要在e-b函数中找到最低点b，与e-w函数一样，现在通过斜率调整b。让这两个调整合成为一个调整过程，不断调整后就可以到达碗装曲面的最低点了。曲面上的梯度也正是“梯度下降”中“梯度”的由来了。

在现代，有基于动量的梯度下降，AdaGrad，RMSProp，Adam，提高了训练效率。

反向传播

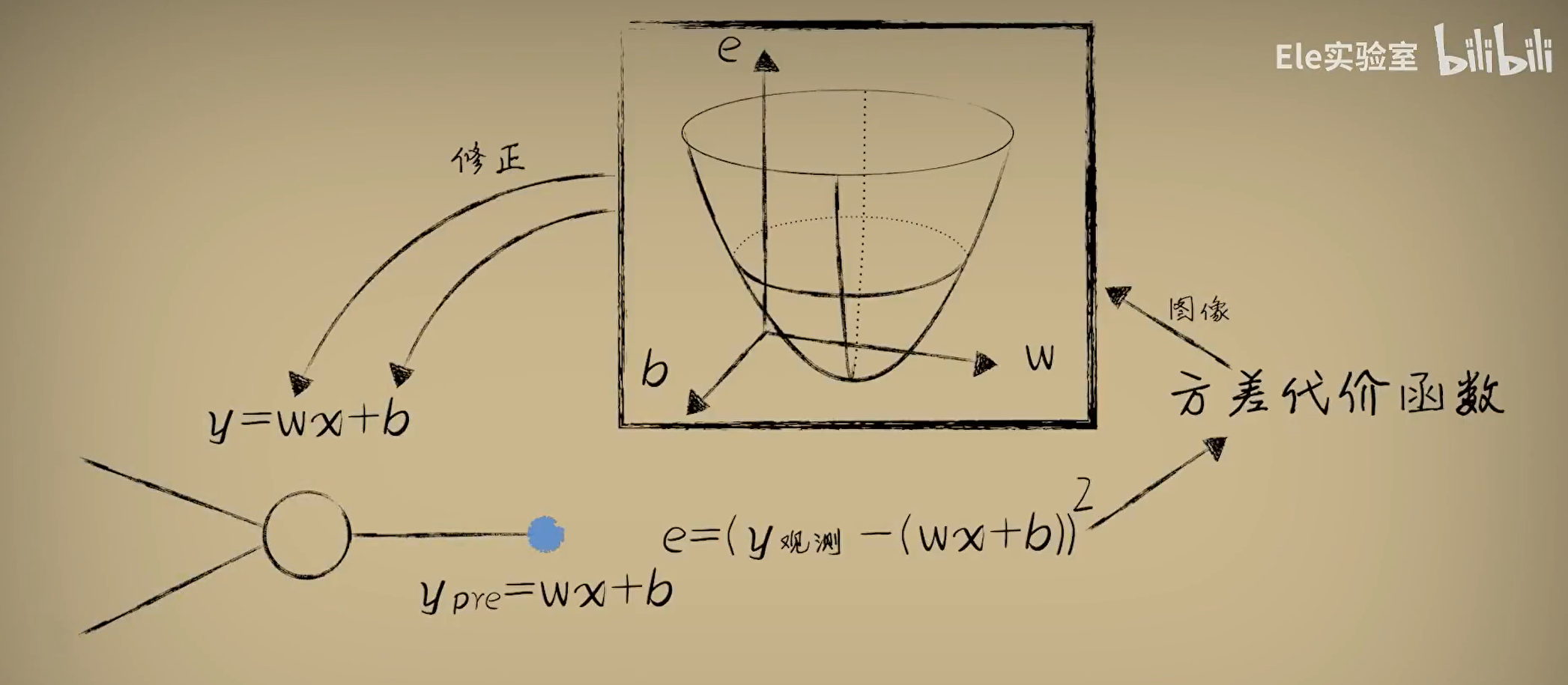
把统计的数据送入预测函数进行预测的过程叫做前向传播，因为计算从前往后。数据通过预测函数完成一次前向传播，就会得到一个预测值，预测值和统计观测而来的真实值之间存在着误差。我们使用方差代价函数来修正预测函数参数的过程叫做反向传播，因为计算从后往前。

不断经历前向传播和反向传播，最终到达代价函数最低点的过程叫做训练/学习。

总结来说：从简单的线性回归开始，数据前向传播进行预测，误差代价反向传播调整权重和偏置参数。这也就形成了现代神经网络工作模式雏形。

激活函数

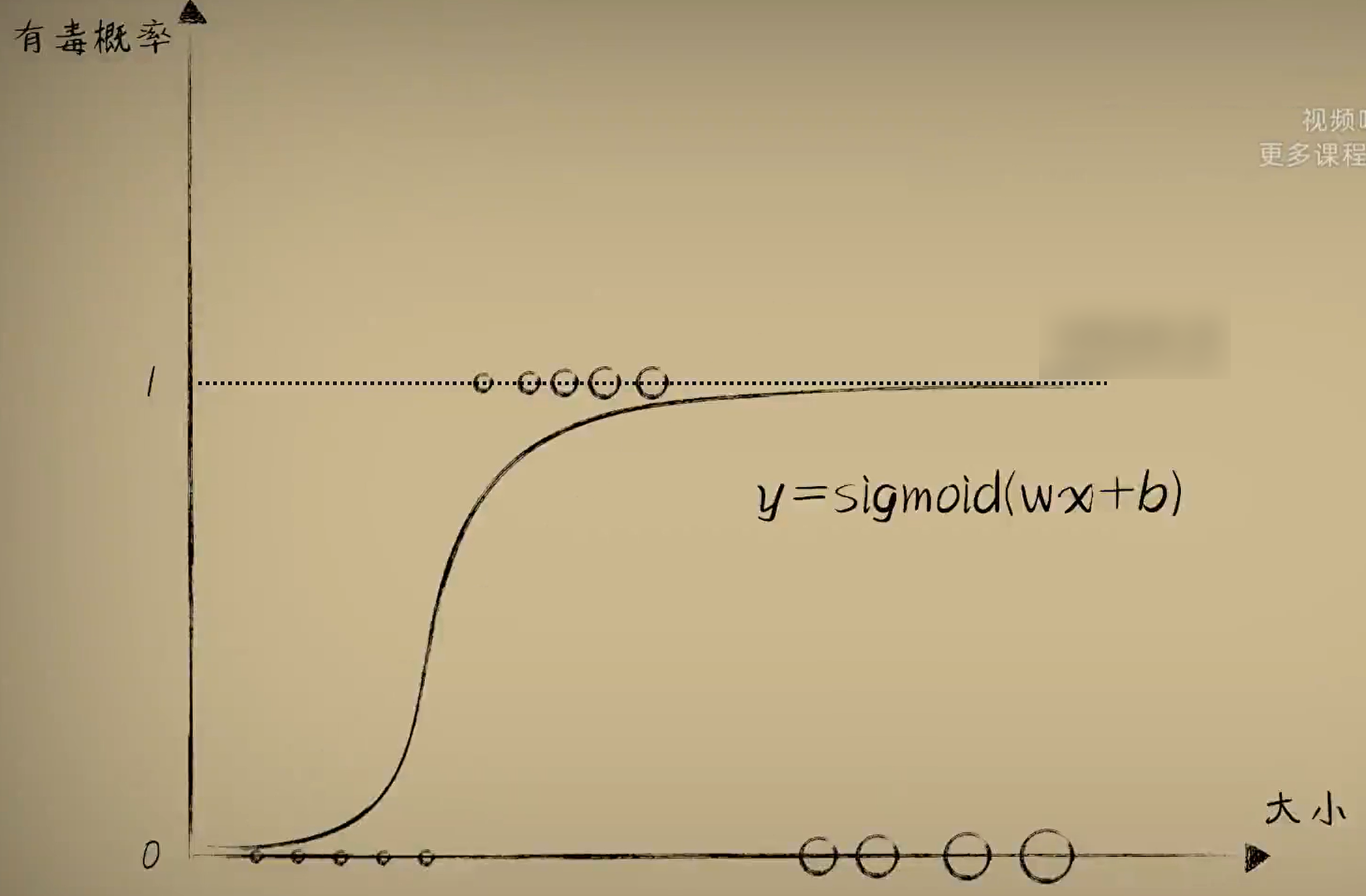
在上面讲到的精确拟合的方式似乎并不是一个智能体思考时常见的方式，我们更常做分类。把豆豆分为有毒/无毒，而不是有毒的概率。那么面对这个分类问题，我们之前的一元一次函数模型固然就废了。若把之前线性函数的结果进入分段函数进行加工，新加入的分段函数就叫做激活函数。非线性的激活函数让神经网络摆脱线性系统的约束，产生了解决复杂问题的能力。

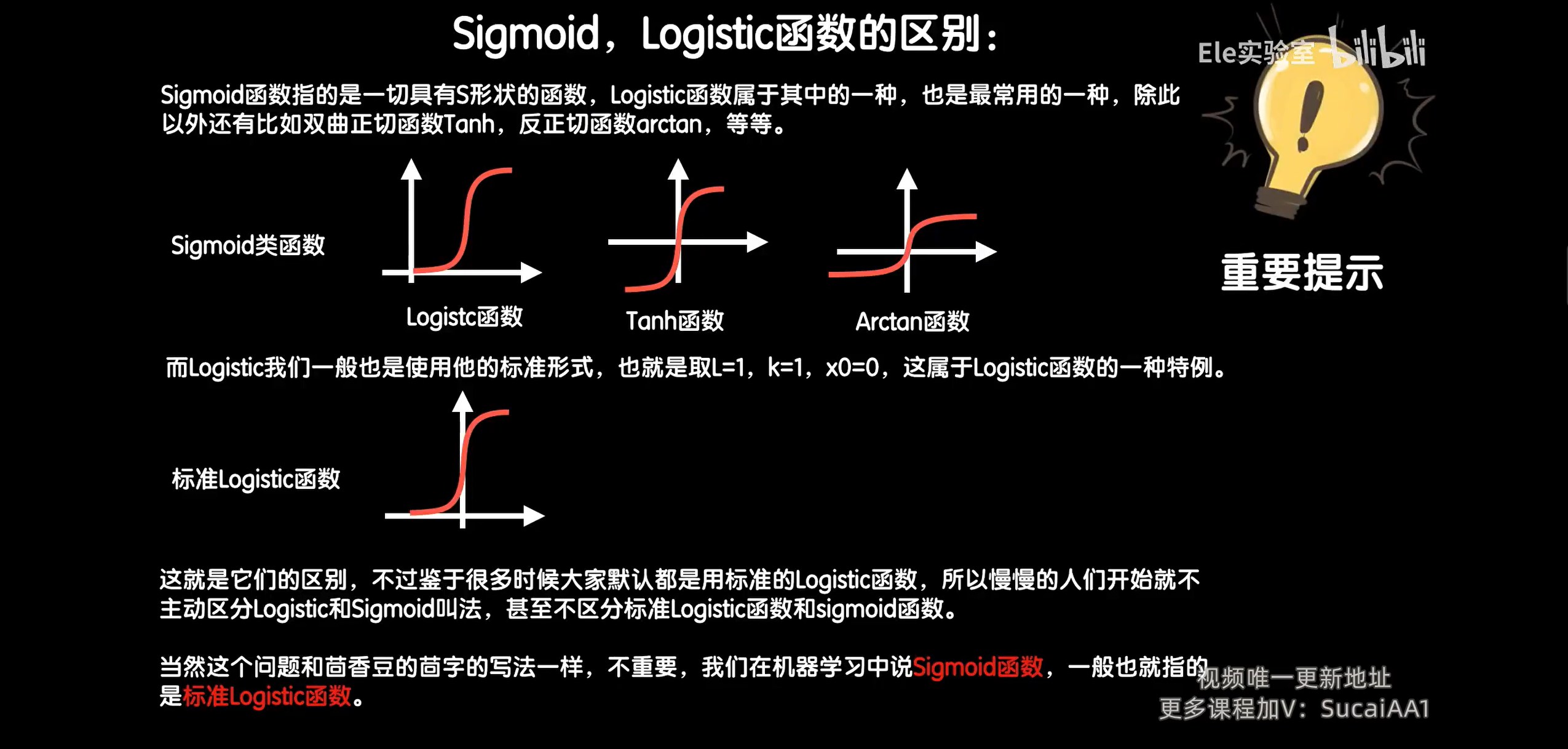
其实Rosenblatt感知器也有激活函数，Rosenblatt感知器中的激活函数是由阶跃函数充当的。它不太好，因为在分界点处没有导数，无法进行梯度下降，另一种更好的s型函数为Logistic函数。这个函数的计算结果在0~1之间。

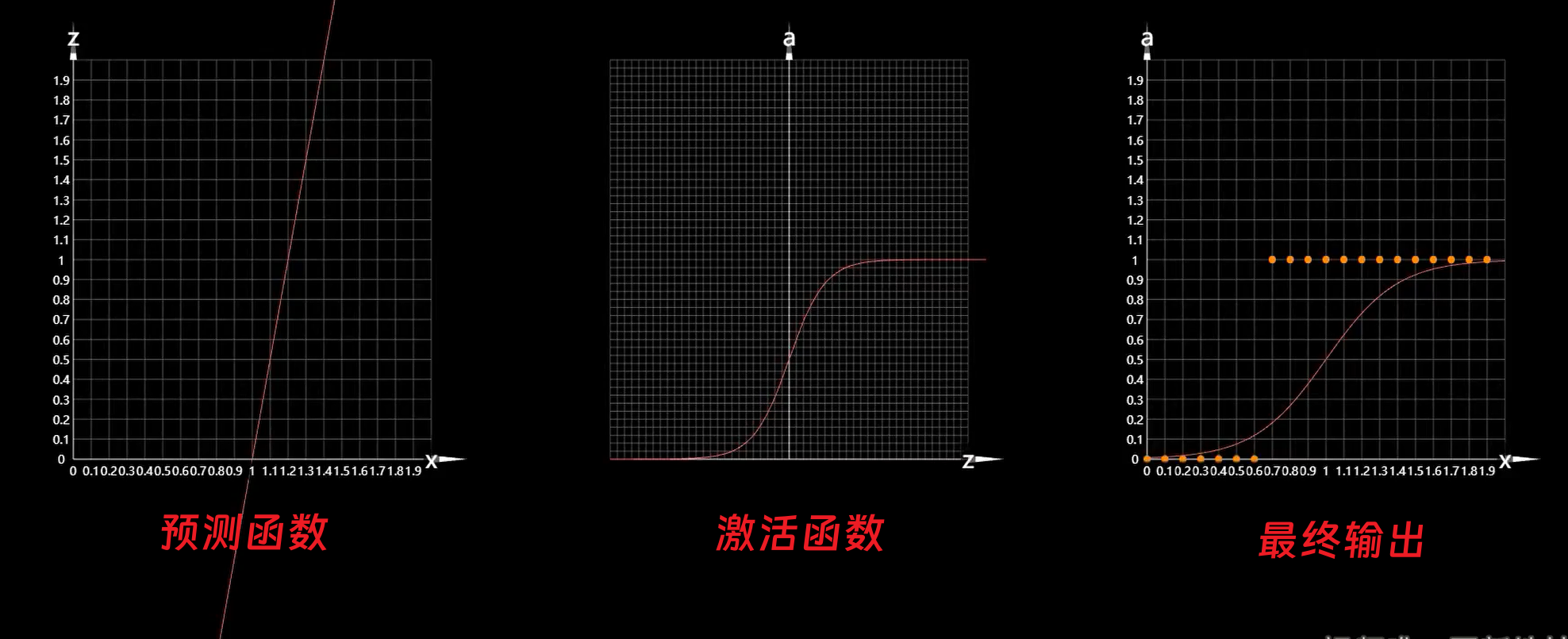
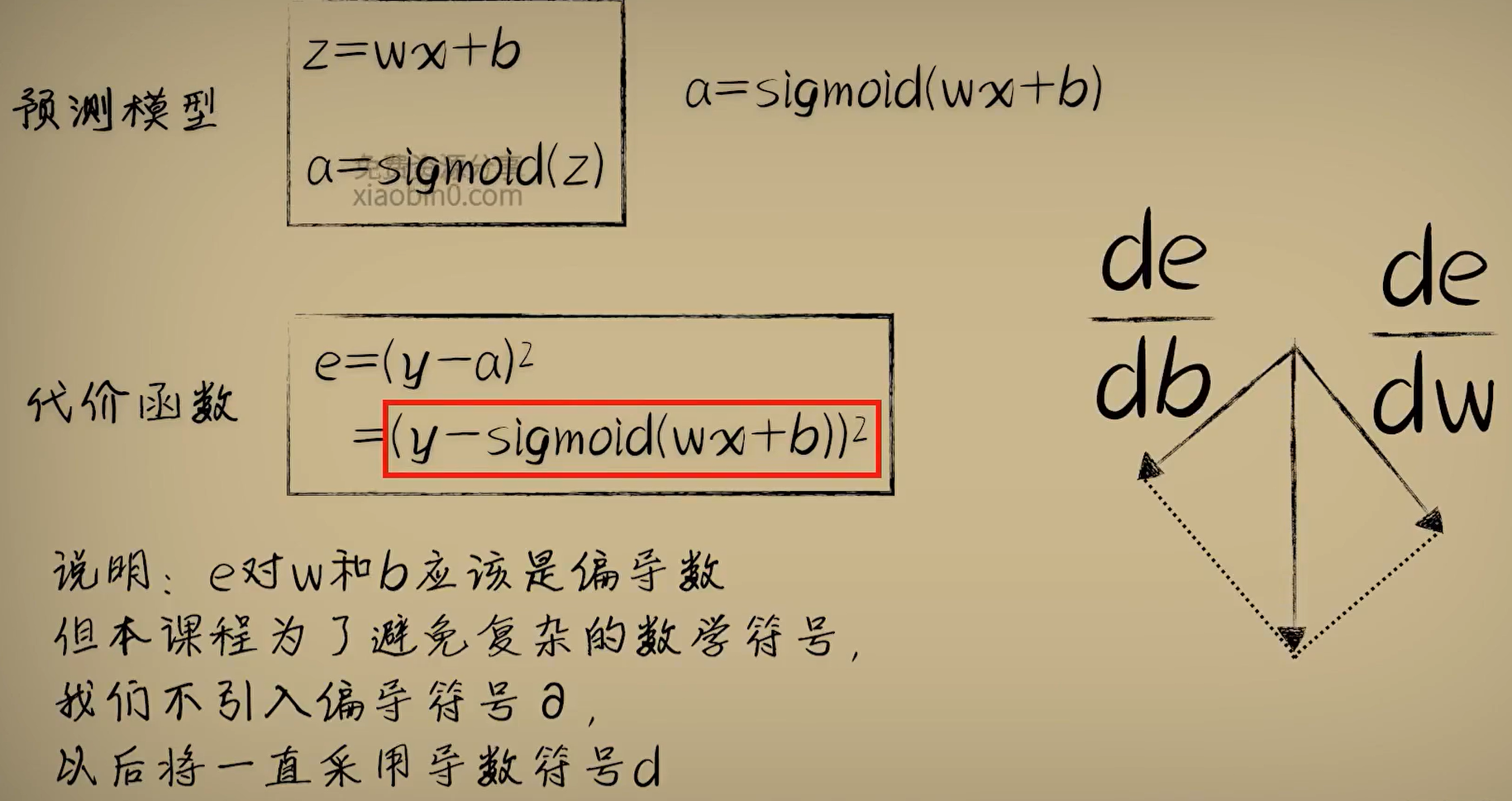
以上是使用激活函数后新的预测模型。这时求导难便成了一个问题。这时可以使用复合函数的链式法则进行简化。

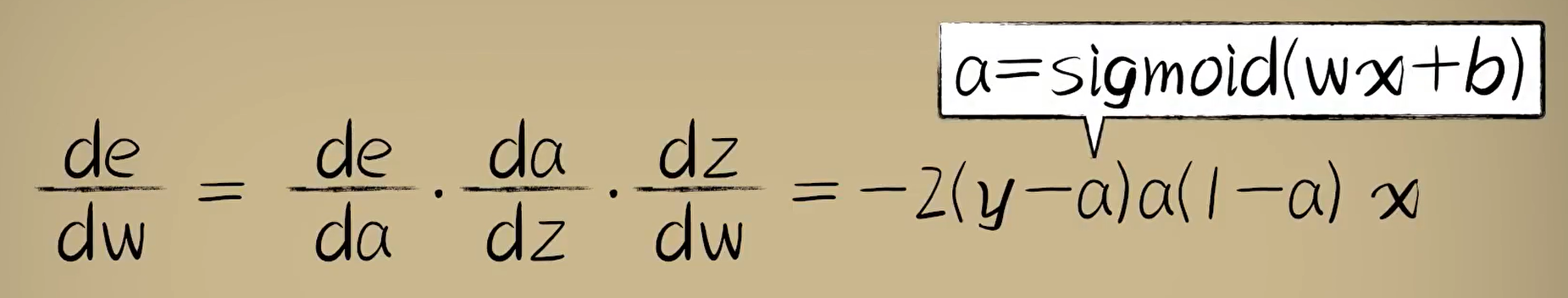
二分类：sigmoid。在后面的在多层神经网络的隐藏层中采用relu激活函数（有效地缓解梯度消失问题）。

隐藏层

经历一段变化后，小蓝又遇到了新的问题。写在豆豆的毒性只在特定大小范围内体现出有毒，这样的话无论是使用单纯的一元一次函数感知器还是加入激活函数，都无法准确的预测当前的豆豆毒性。如何让预测模型产生山丘一样的曲线？是时候让神经元形成一个网络了。

现在多添加了两个神经元，将x分别输入两个神经元进行计算，结果送入第三个神经元，最后输出。调节一下这三个神经元的参数（如上动图），最终分类成功。也就是说把输入分为两个部分，分别对两个部分进行调节然后再送入最后一个神经元，让整体神经网络形成单调性不唯一的更多变的函数，从而具备了解决更多复杂问题的能力。而中间这些新添加的神经元节点也称之为“隐藏层”。隐藏层让神经网络能在复杂的情况下依旧Working。

ChatGPT的解释：在神经网络中，隐藏层（Hidden Layer）是介于输入层和输出层之间的一层或多层神经元组成的层次。每个隐藏层包含许多神经元（也称为节点或单元），这些神经元接收来自前一层（输入层或上一隐藏层）的信号，并将它们传递到下一层。隐藏层的存在使神经网络能够学习复杂的非线性关系，从而提高对输入数据的表示和模式识别能力。在深度神经网络中，存在多个隐藏层，这些隐藏层逐渐将原始数据进行抽象和转换，从而生成更高层次的特征表示。隐藏层中的每个神经元都与前一层中的所有神经元相连，并具有权重，这些权重决定了信号在网络中传递时的影响程度。隐藏层的激活函数通常用于引入非线性变换，从而使网络能够学习非线性函数。

在之后会给神经网络纵向延伸，添加更多隐藏层，输入通过这些隐藏层，被一层又一层的隐藏层不断抽象和理解，提取出微妙特征，让神经网络变得更智能。一般把隐藏层超过三层的神经网络称为深度神经网络。

机器如何面对越来越复杂的问题

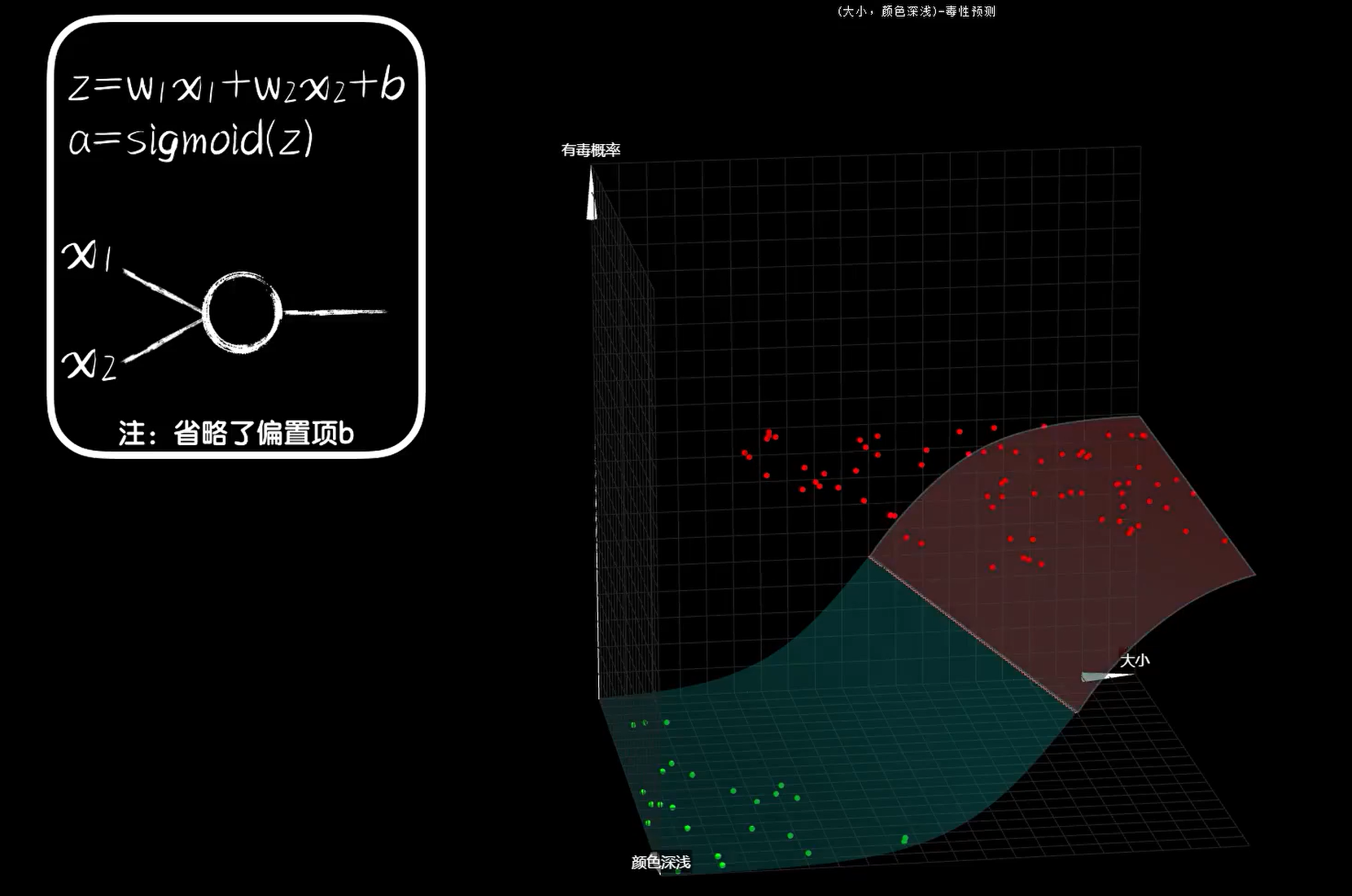
对于豆豆的问题，现实世界中往往并不是那么简单，豆豆的毒性不仅与大小有关，也和颜色深浅有关，此时的预测函数为二元一次函数，图像为三维图像。我们找到预测曲面上预测值为0.5的点连接起来，这条线就是地理意义上的等高线，在这里叫做类型分割线。

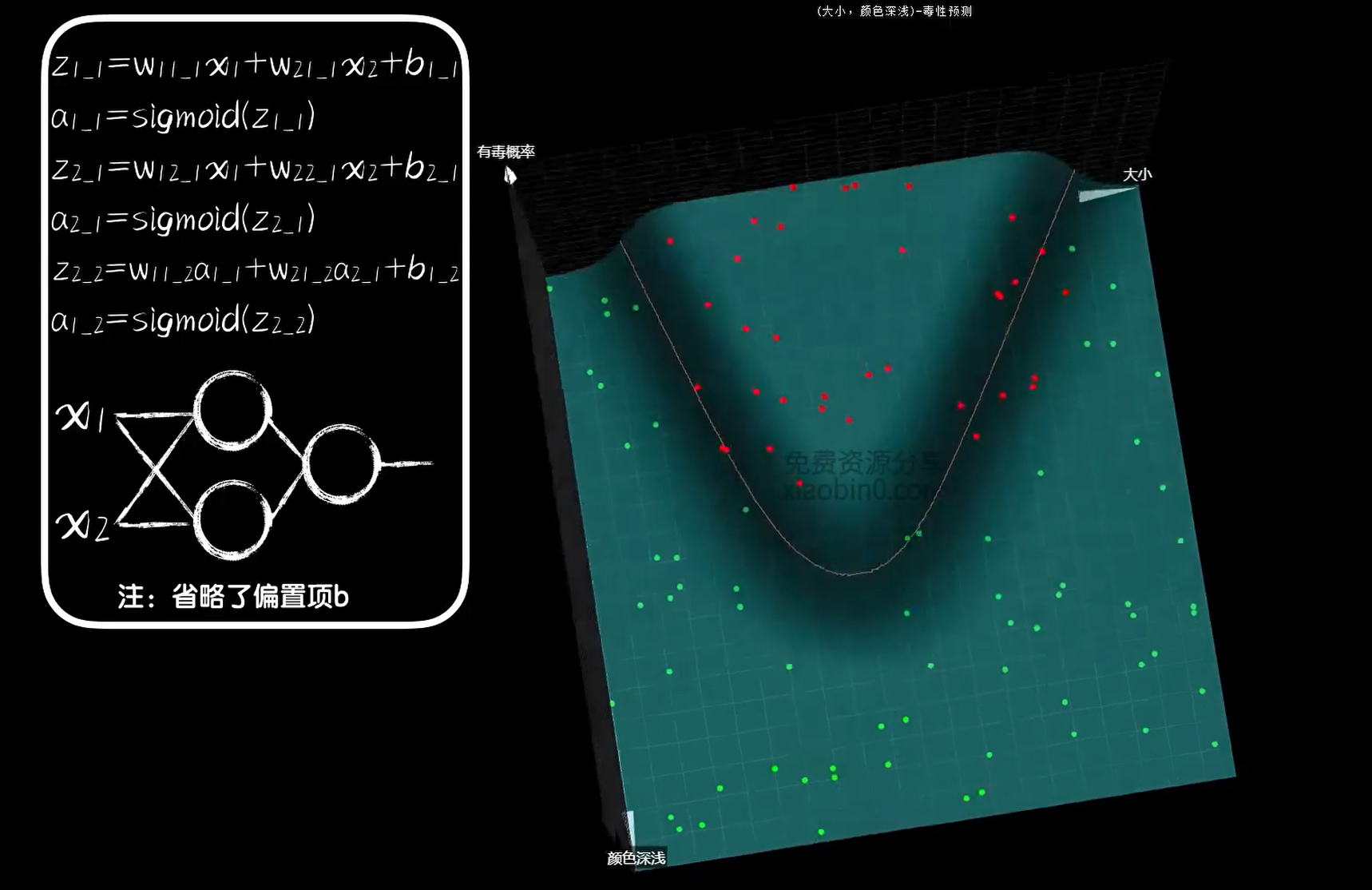
若其有毒仅分布在一片区域内，也就是说想要让类型分割线为曲线，那么建立之前说到的隐藏层即可解决这个问题。

当问题数据特征越来越多，也就是说输入越来越多时，我们不得不再添加一个维度去描述预测函数的图像，四维图像？太抽象了。所以我们将在后面引入向量和矩阵，并使用Keras框架搭建神经网络，我们不再需要考虑前向传播，反向传播，梯度下降等等，但是唯一逃脱不掉的就是向量和矩阵。

向量和矩阵

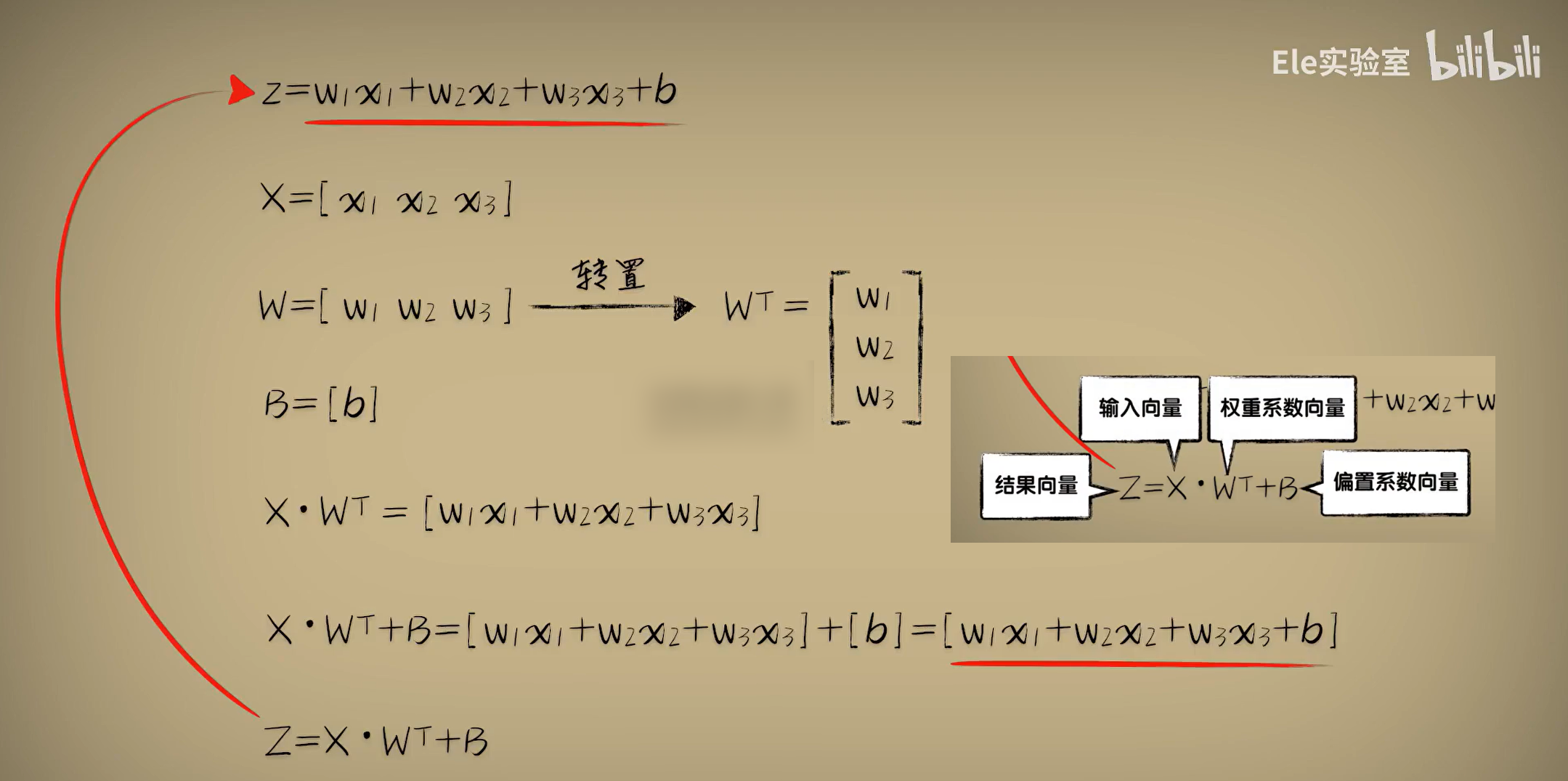
对于程序员来说，向量就是一维数组，矩阵就是多维数组。我们需要使用数学家的角度来看待它们，它们就是数学中的一种工具。我们给向量定义转置和点乘的规则。那么预测函数最终被表示成Z=X·W的转置+B，ZXWB均为向量。若是1000元一次函数，使用向量的优点将被体现的淋漓尽致，预测函数还是Z=X·W的转置+B，只不过X和W的元素数量为1000。

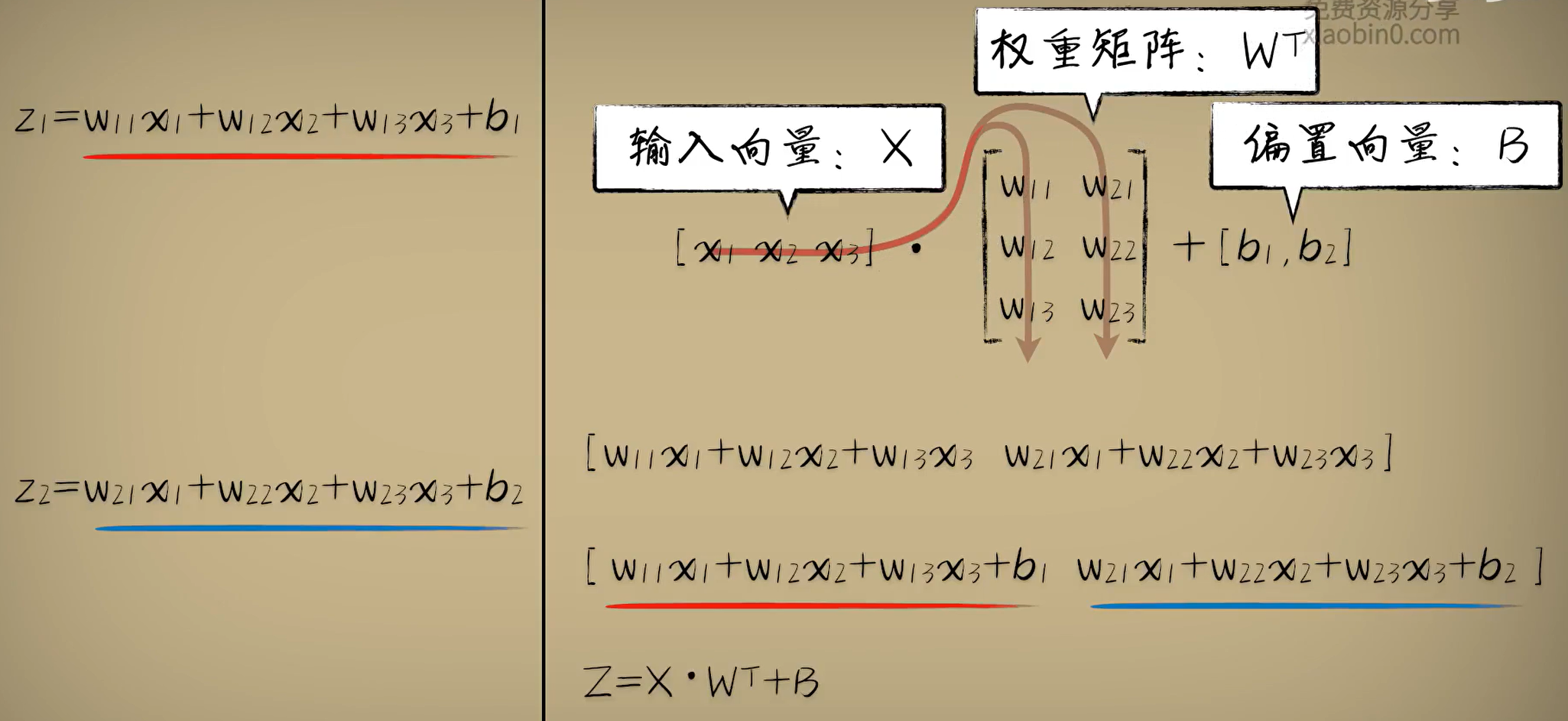
如果输入的数据送入一组函数进行运算（例如新增隐藏层），单个向量貌似也不是很方便了，为什么不把它们放到一起呢？矩阵可以看作是多个向量组成的，其转置操作也是相同的。这时预测函数还可以使用Z=X·W的转置+B来表示，只不过W是2*3的矩阵。

Keras框架

深度学习就是不断增加一个神经网络中的隐藏层数量，让输入的数据被这些神经元不断抽象和理解，最后得到一个具有泛化能力的预测网络模型，把隐藏层超过三层的神经网络叫做深度神经网络。

神经网络入门神器：https://playground.tensorflow.org/

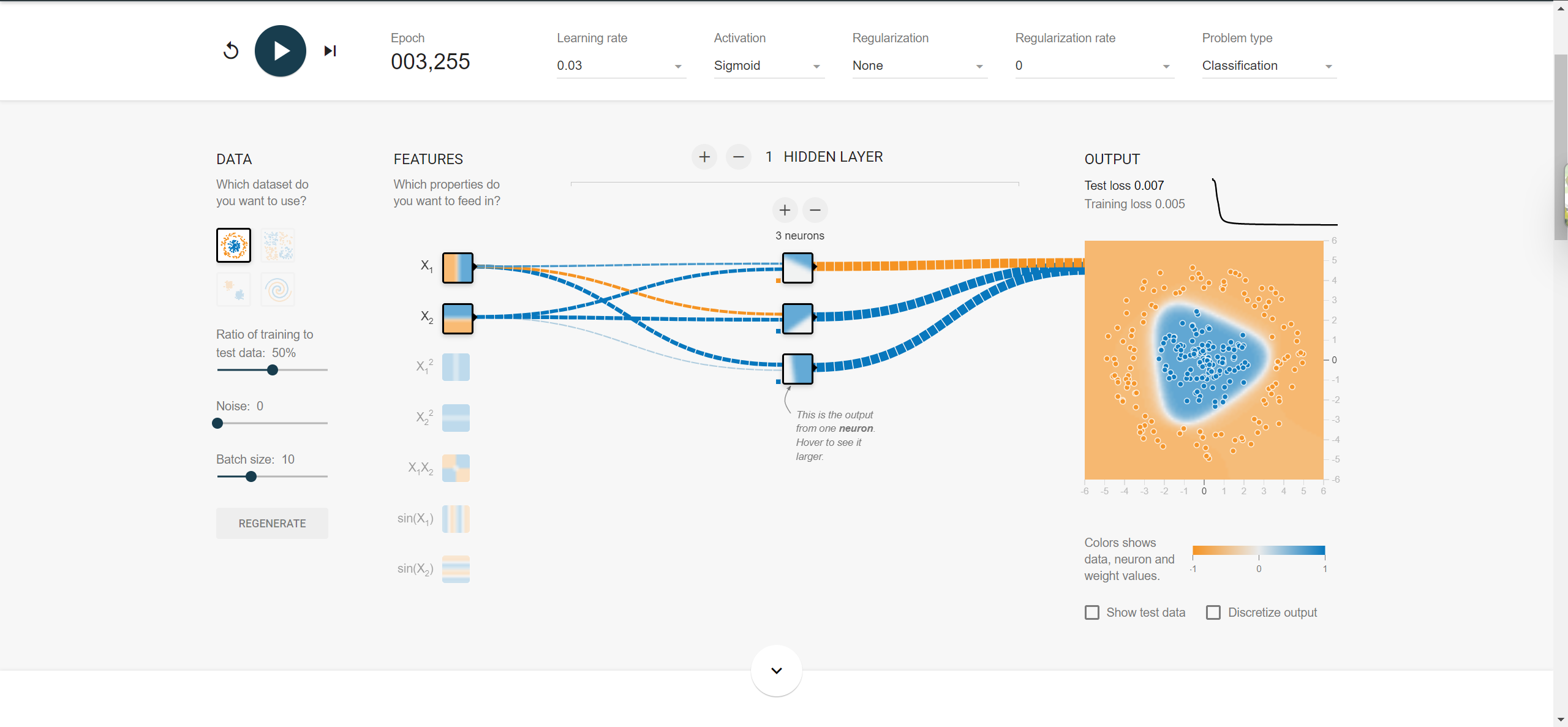
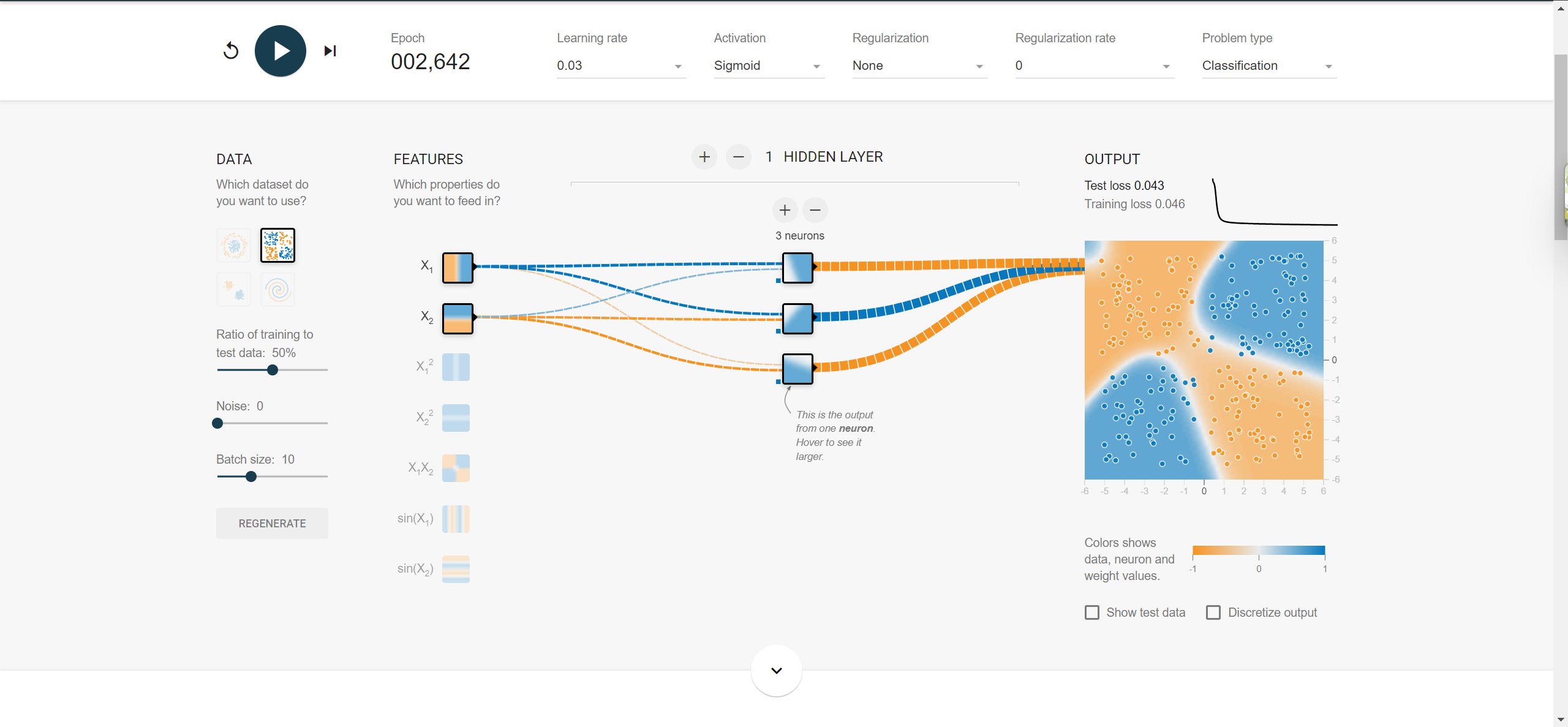
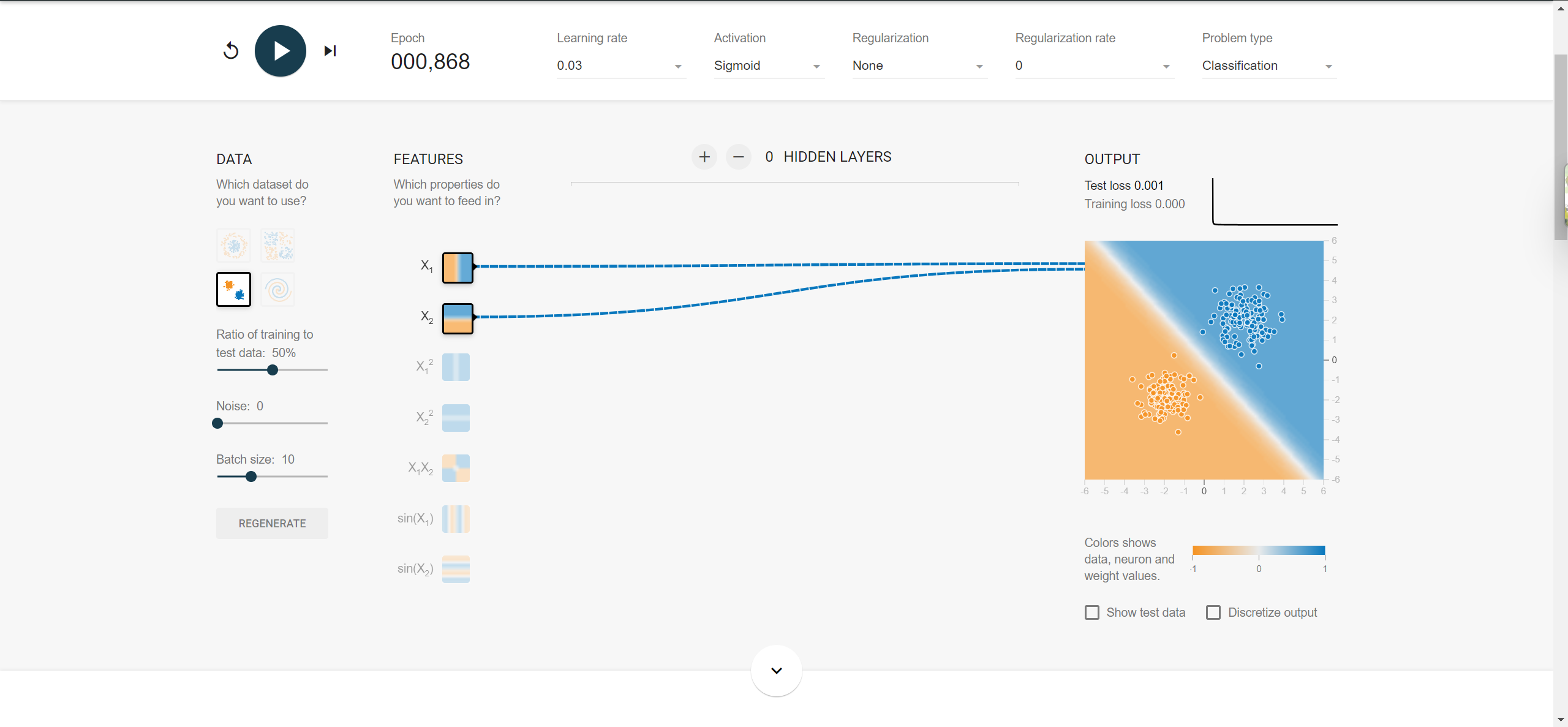
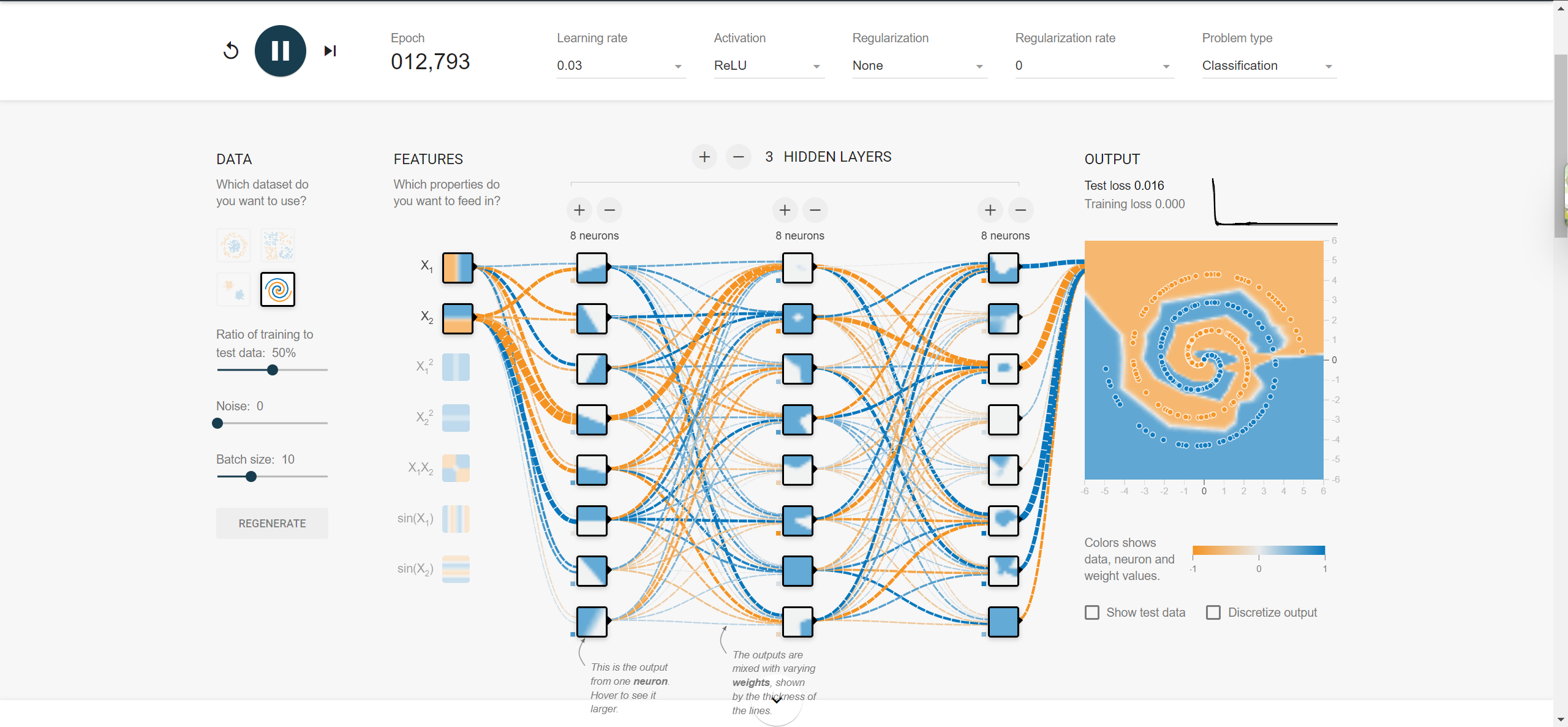
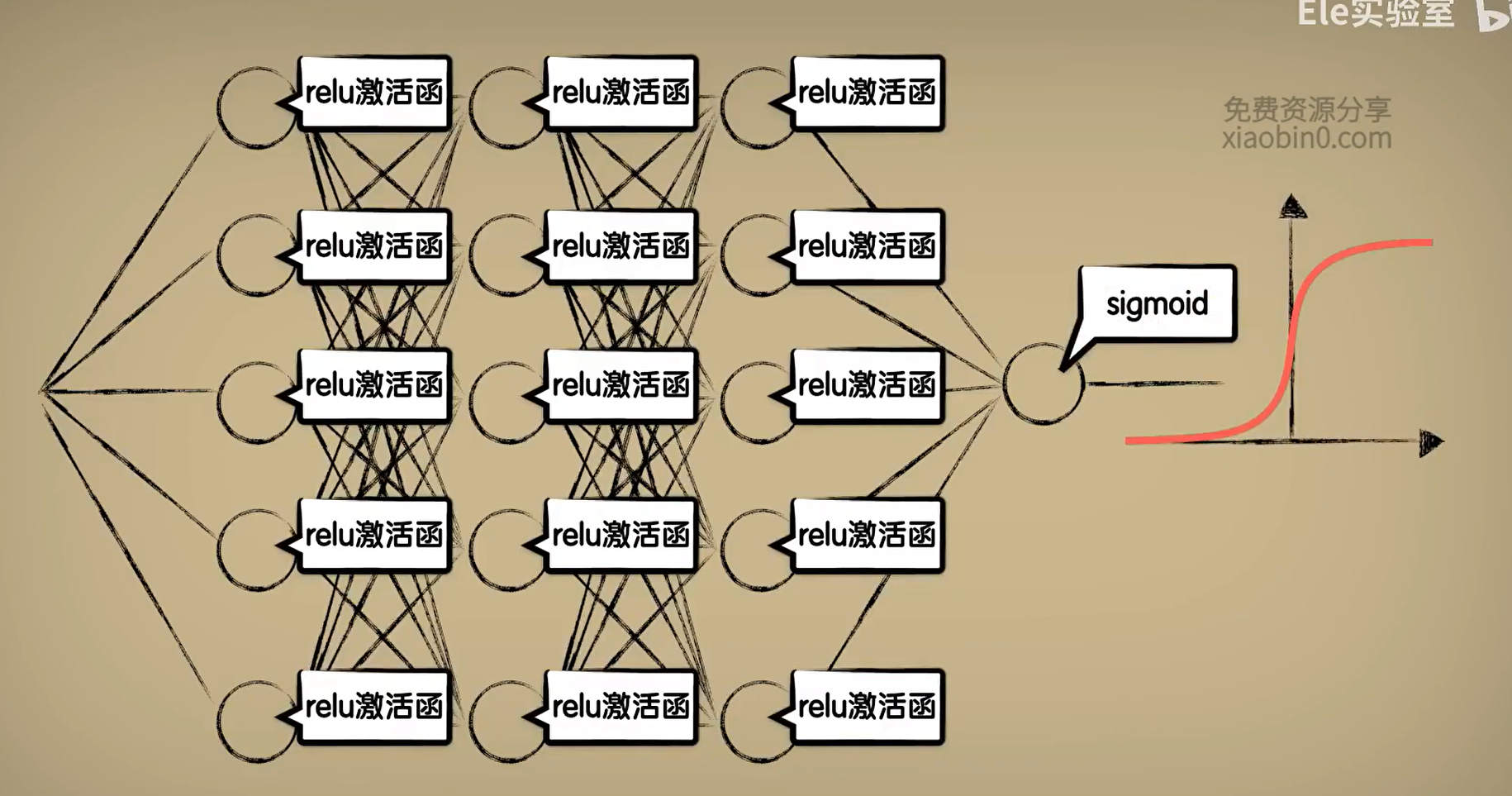
多层神经网络的隐藏层中采用relu激活函数。有效地缓解了sigmoid激活函数在深度神经网络中梯度消失的问题。

Keras框架可以让我们更轻松的搭建神经网络。

计算机视觉

手写体识别是计算机视觉中经典的“Hello World”。mnist数据集图片采用28x28的灰度图。亮度为0~255。使用神经网络识别手写的0~9，再适合不过了。

图片是一个方形的像素灰度值的集合。把28x28的二维图像拉出到一个长度为784一维数组（向量）。我们只需要把每个图片都变成784个元素的向量，然后依次送入神经网络训练即可。人们有了一定的成果但是不是很好。

考量一个模型的好坏：测试集高准确率！

欠拟合：孩子训练集准确率低，多半是废了。

训练集和测试集准确率都很高相差不大！泛化能力好好好。

过拟合：训练集准确率高，测试集准确率低。解决：调整网络结构，L2正则化，节点失活。

mnist数据集有6万个训练集样本和1万个测试集样本。人们发现用全连接神经网络做mnist数据集识别和其他图像识别时，尽管把网络堆叠的越来越深，神经元数量也越来越多，也用尽了各种防止过拟合的方法，但网络泛化能力也很难有突破。直到最早的卷积神经网络，测试集准确率达到了99.2%。

卷积神经网络

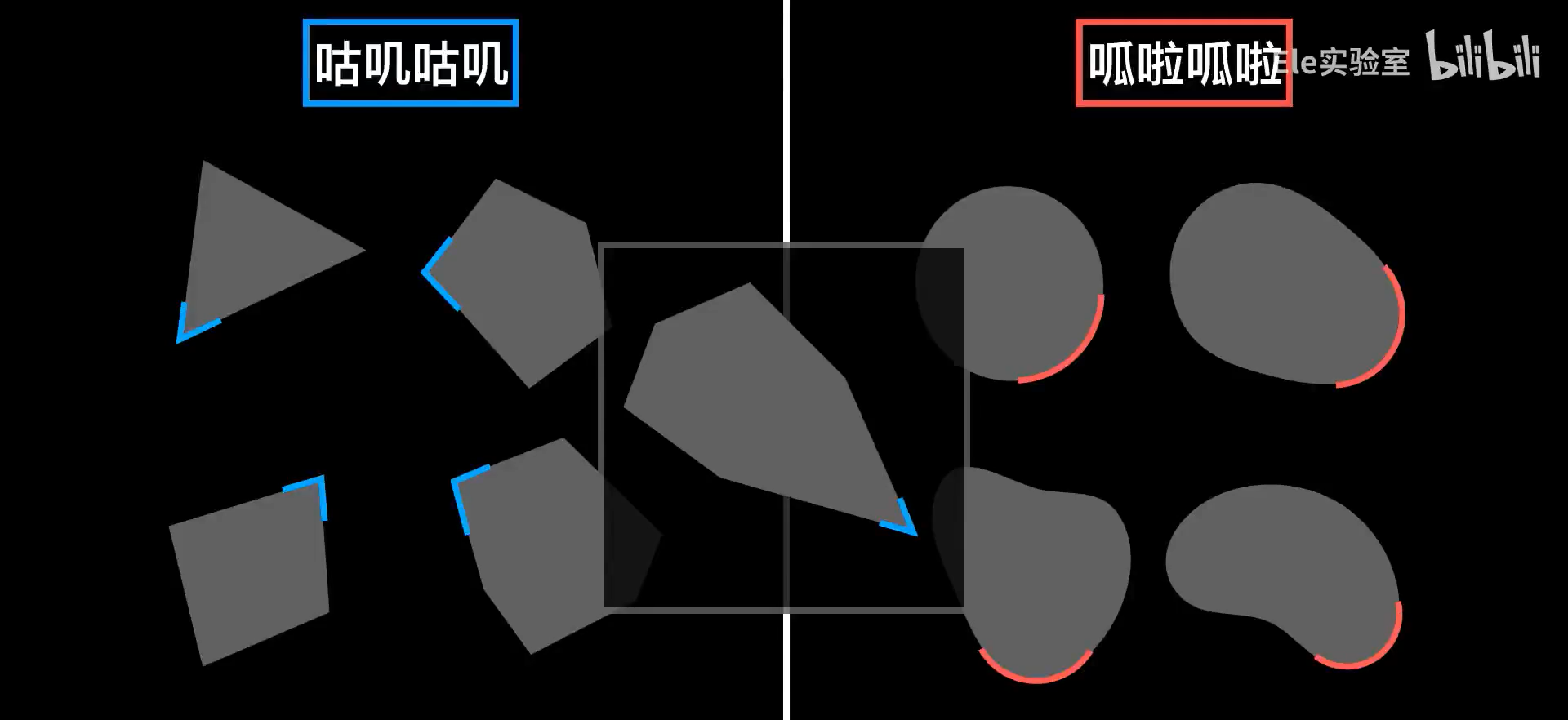
卷积是怎么工作的？把一个图像的像素变成数组之后人不可能看出图像是什么内容。而还原之后才能识别出内容。人在识别图片时会提取轮廓，颜色，花纹等等特征。图像作为二维物体，在二维平面相邻像素之间是存在关联的，强行降维打击就失去了这些特征。

卷积运算的过程是这样的，例如一个8*8像素的图片。手动构建一个3*3的小矩阵（卷积核/过滤器），从图片左上角开始，把小的罩在大的上面，把对应的元素相乘，结果加到一起得到新的一个值。每一行都是这样，最终形成了一个6*6的新图片，由于灰度值最大是255，所以把超过255的都变成255。

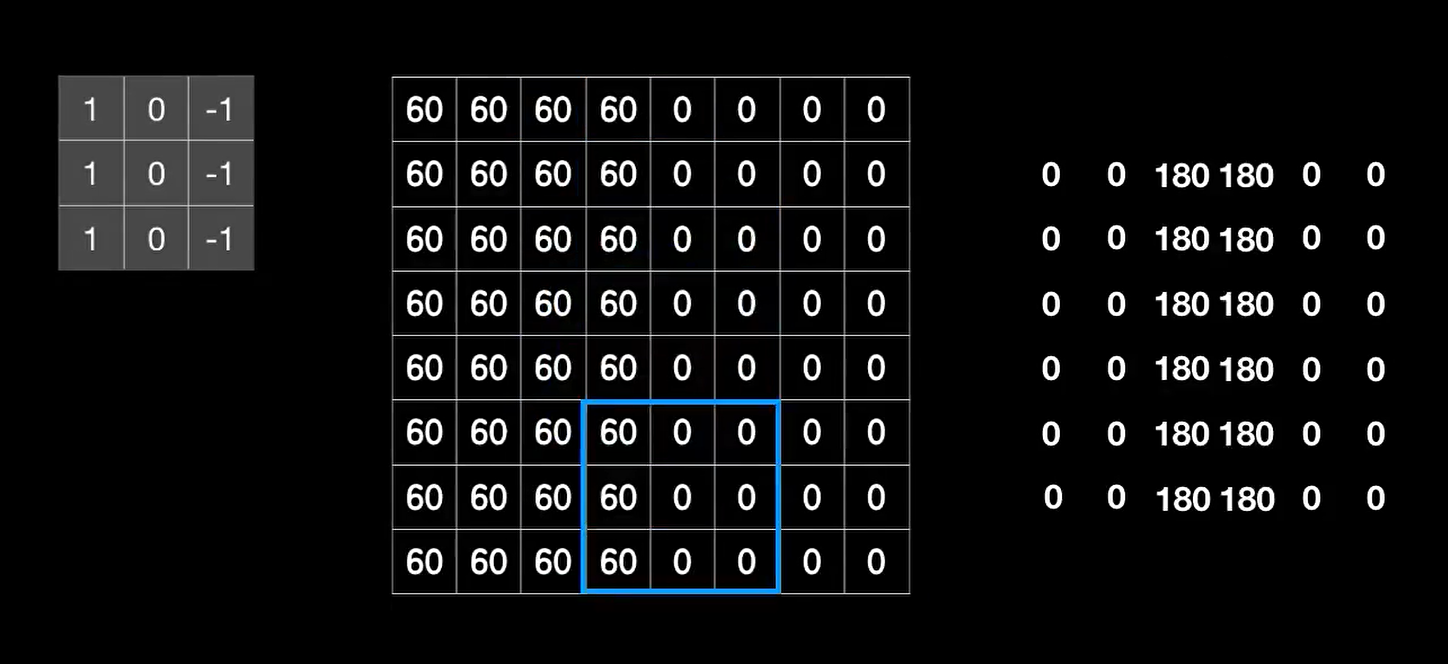
这个卷积核用于提取垂直边缘，原理如上图所示。卷积核在垂直方向上左右对称的两列值是相反数，所以遇到灰度值相近的3*3像素块，就会相互抵消最终为0。

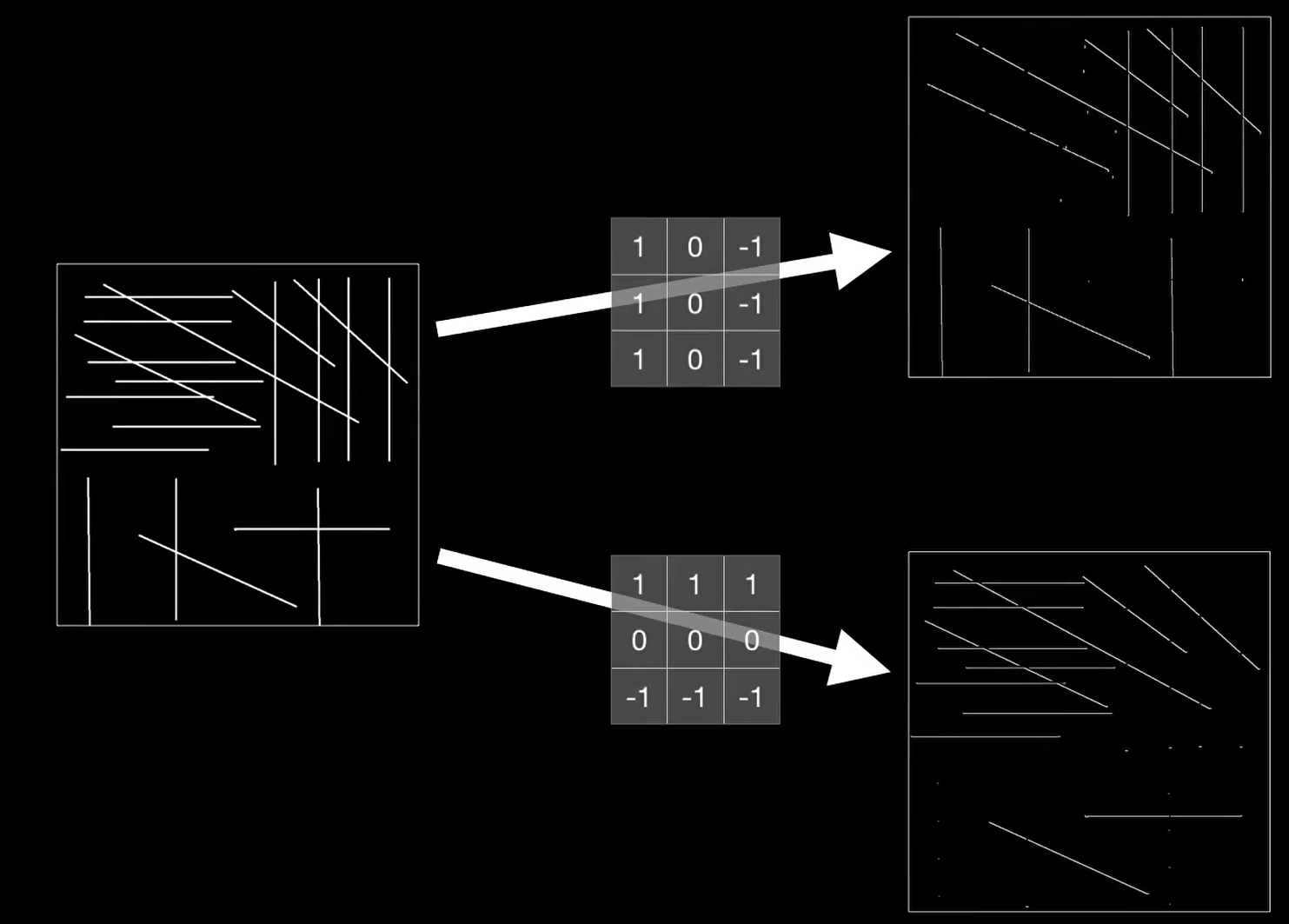
图像识别实战

卷积核的值设置为多少合适呢？随机初始化即可，其实卷积核的值也是通过学习/训练得来的。

卷积层除了对数据提取方式不同以外，其他部分和一个全连接层没有什么区别。如图，误差代价如何传到卷积层呢？实际上，我们完全可以从某种角度把卷积层发生的事情，类比到普通神经元。

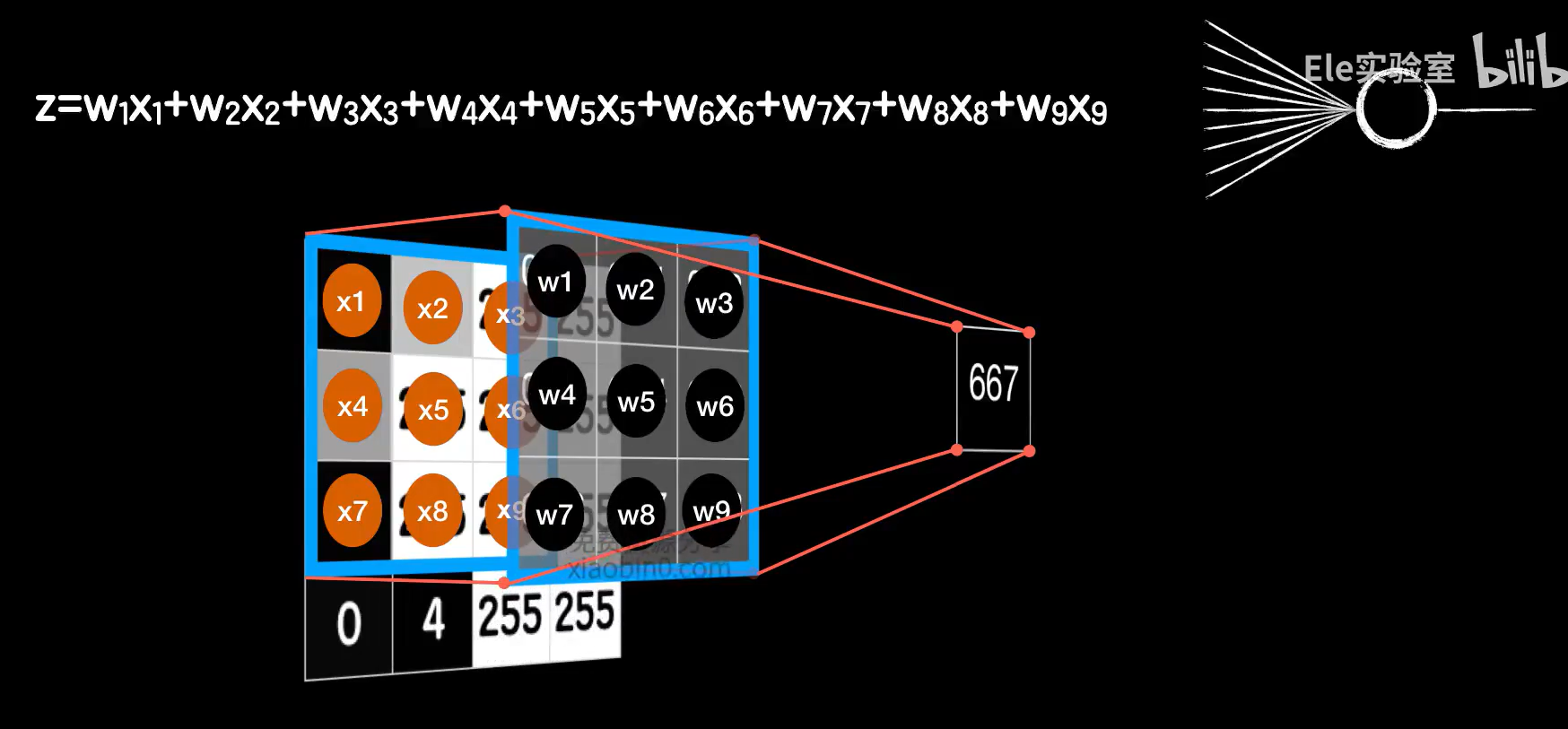
如图，可以把原图中被卷积核包括的部分看作9个（卷积核为3*3的情况下）输入数据，把卷积核中的值看作是权值参数w，最后运算的结果便是一个输出。这样就是9个输入，1个输出的普通神经元的线性运算部分。一般来说还需要给神经元的线性函数加上偏置项b，所以我们需要给卷积的结果加上b，加入激活函数进行非线性运算后，这样就真的可以类比到普通神经元了。

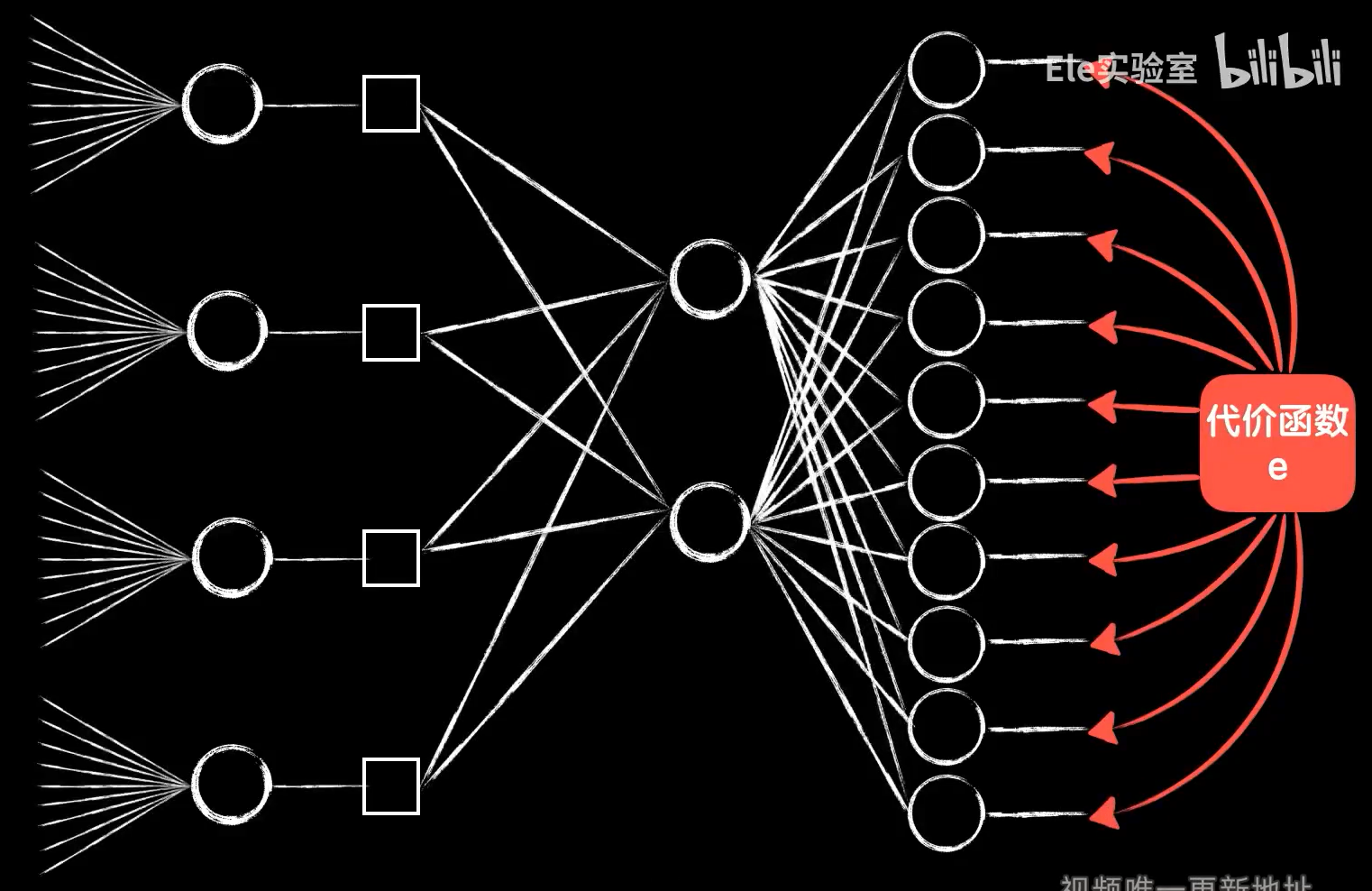
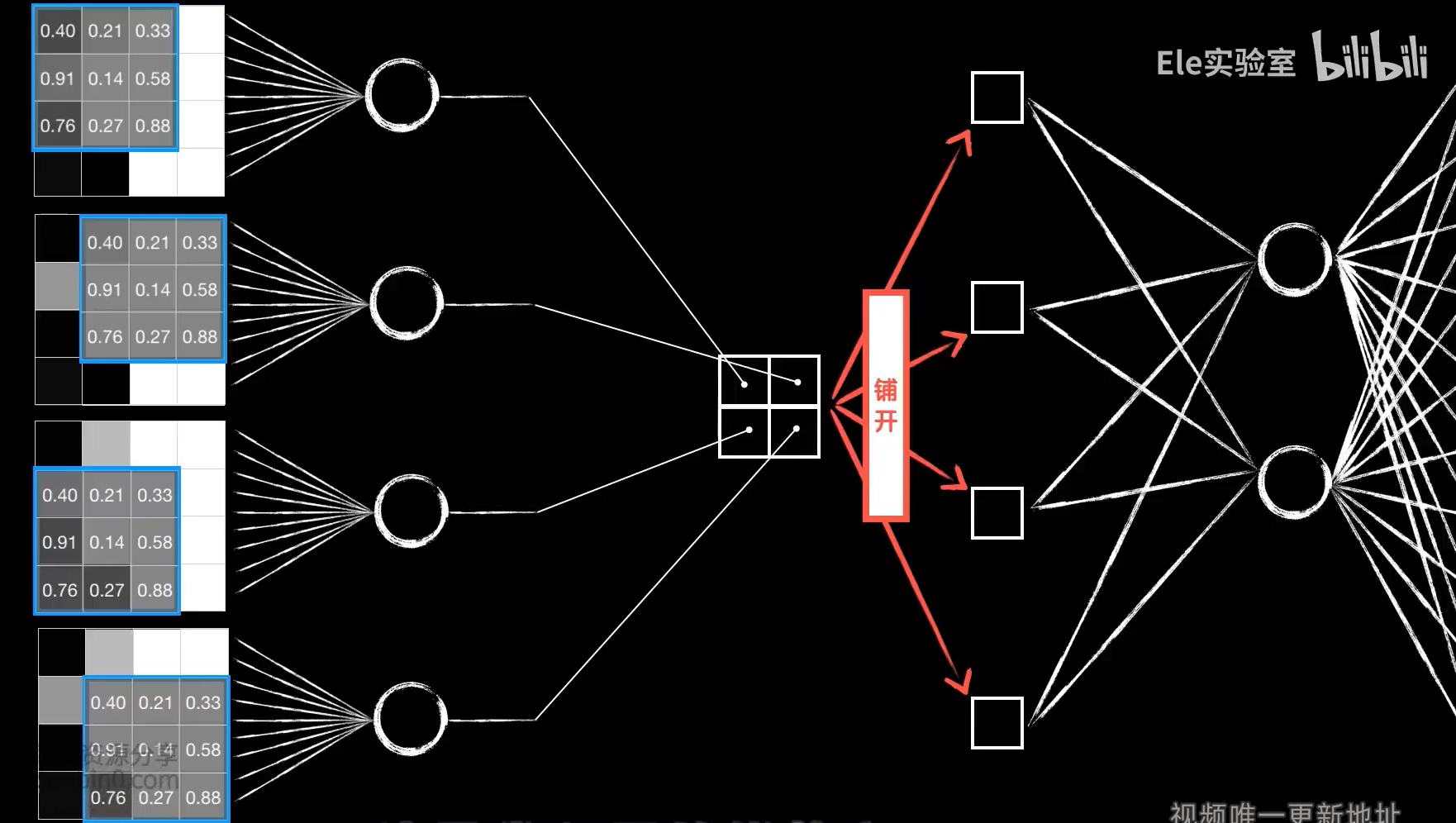
细节：四个神经元的输出是根据卷积过程排列而成的二维结构，送入后面的全连接层需要平铺开。四个神经元的输入并不相同，是图片的不同区域，最重要的是，这四个神经元的权值参数并不是独立的，而是相同的，因为权值参数就是卷积核中的值，同时偏置项b也是一样的，这也就是参数共享。这是卷积层的优势之一。为什么卷积神经网络的效率和泛化能力高，就是因为参数共享使得卷积层的参数比全连接层少很多。（例如mnist数据集中28*28的图片，全连接层需要(28*28+1)*4=3140个参数，而3*3卷积核的卷积层也仅仅需要3*3+1=10个参数）

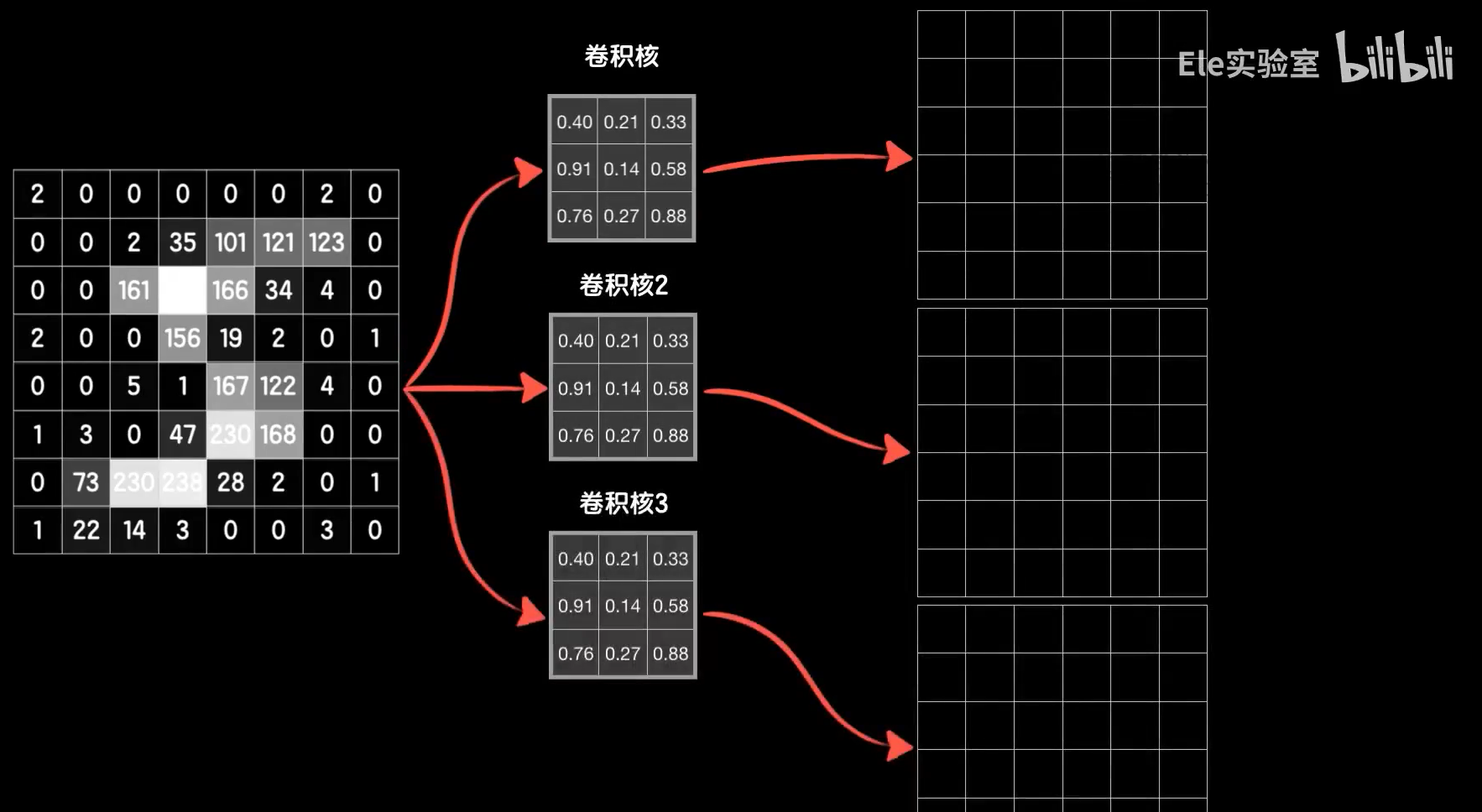
一个卷积核训练的结果仅提取了图像的一种特征，还不够，需要提取多种特征需要多个卷积核。一个卷积核卷完一个图像会生成一个二维图像，那么多个卷积核卷完一个图像就会得到三维的张量。把三维张量铺开得到一维向量输入后面的全连接层训练即可。

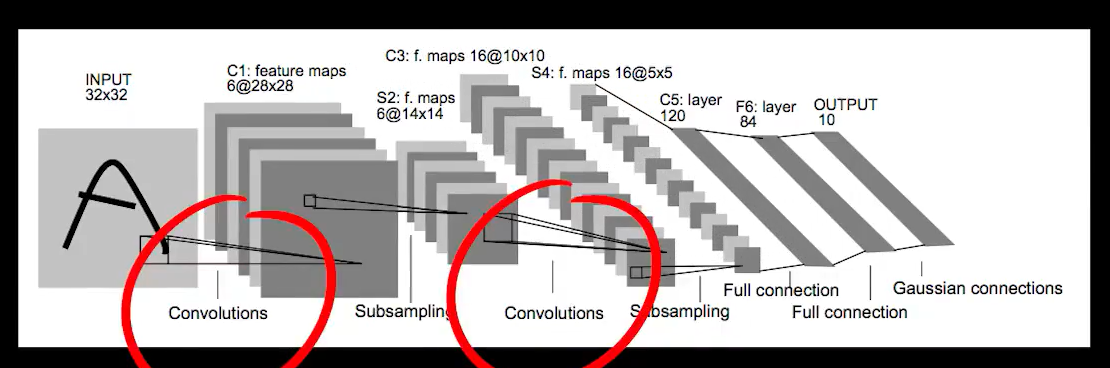
但是在送入全连接层之前，能不能继续卷这个三维的张量呢？LeCun在1998年提出的LeNet-5卷积神经网络结构，这个结构中卷了2次之后再送入全连接层。

在三维数据上使用三维卷积核。三维卷积操作如上图所示，三维卷积操作的输出通常为三维数据，但是为了能让卷积核罩住数据，进而输出二维数据，所以三维数据的宽（通道数）为卷积核的第三个维度。

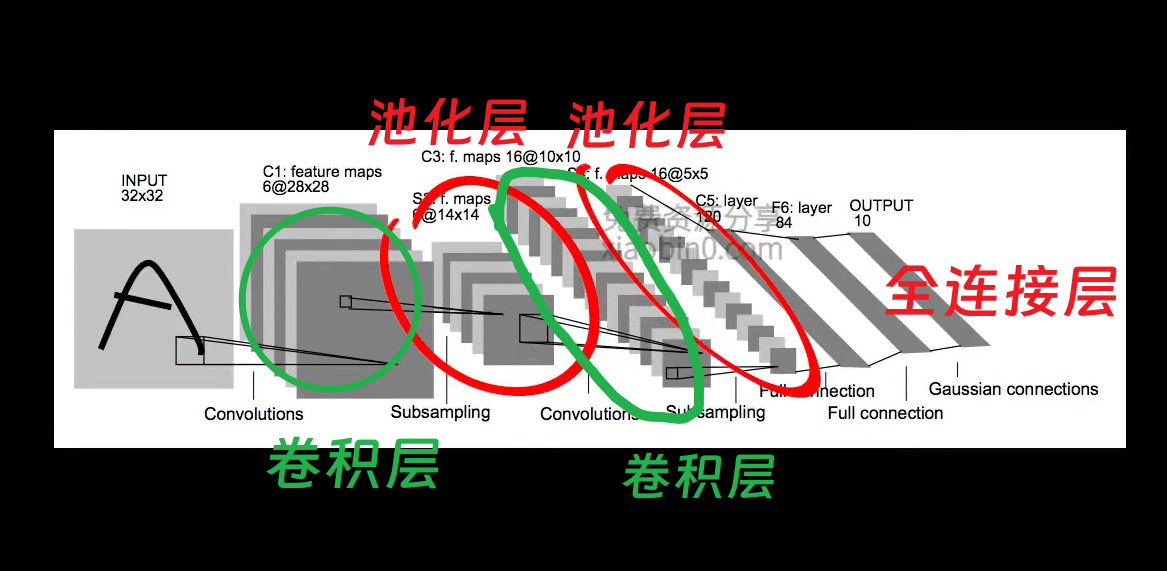
而在LeNet-5中除了我们认识的卷积层和全连接层外，在卷积层后的是池化层。池化层是这样的：从数据的左上角开始，框出一个区域，求出这个区域数据的平均值（或者其他方式，上图是平均值），然后向右移动，到头后到下一行依次计算。取平均值方式叫做平均池化，取最大值方式叫做最大池化。三维池化与上面说到的三维卷积相似，不再赘述。在很多经典的卷积神经网络中卷积层后往往会加入池化层，但这并不是必须的。池化操作是固定的套路，所以在反向传播中它并不需要学习任何参数。